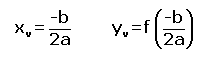Las parábolas
En el artículo de hoy vamos a estudiar la representación de las funciones cuadráticas, es decir las ecuaciones de segundo grado. Teniendo en cuenta que las gráficas de las ecuaciones de segundo grado corresponden que las parábolas, en este post, vamos a estudiar los elementos característicos de estas.
REPRESENTACIÓN
Comenzaremos con los primeros pasos que vamos a tener en cuenta para llevar a cabo la representación de una función cuadrática, que como sabemos es de la forma:
1º) En primer lugar, nos fijaremos en el signo del coeficiente de la x de grado 2, es decir, en el signo de a. Dependiendo de su signo podremos saber la forma que tiene la parábola:
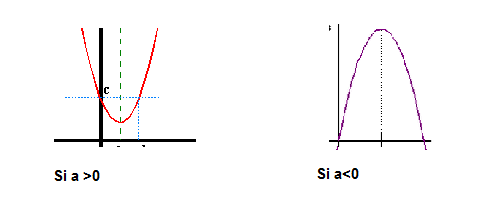
Si a>0, podemos decir que la parábola tiene forma de U.
Si a<0, diremos que la parábola es la inversa de una U.
Como podemos observar en la siguiente imagen:
2º) Uno de los elementos más característicos en las parábolas es el vértice, que a su vez corresponderá con el máximo de la función cuando a0.
El vértice es un punto más de nuestra función, por tanto tendrá una coordenada x, y una coordenada y. Para hallar las coordenadas del vértice, utilizamos la siguiente fórmula:
3º) Si trazamos una recta vertical por el vértice, obtenemos el eje de simetría de nuestra parábola.
Es decir el eje de simetría es x=-b/2a.
4º) El último elemento característico en las parábolas son los puntos de corte (aunque no existirán siempre, ya que depende de la forma que tenga nuestra parábola).
-Punto de corte con el eje OY: para hallar los puntos con este eje, tenemos en cuenta que x=0, por tanto sustituyendo en nuestra función obtendremos el punto de corte:P (0;f(0)) (sólo existirá uno)
-Puntos de corte con el eje OX: para hallar los puntos de corte con este eje, ocurre lo contrario que en el caso anterior, ahora tenemos que y=0, y para halla los puntos de cortes tendremos que resolver la ecuación de segundo grado, es decir, f(x)=0.
Pueden ocurrir tres casos dependiendo de las soluciones de la ecuación:
1. Si la ecuación tiene dos soluciones: x1,x2, existirán dos puntos de corte: P(x1,0) y Q(x2,0).
2. Si la ecuación tiene una sola solución:x, existe un sólo punto de corte: P(x,0), que además coincide con el vértice.
3. Si la ecuación no tiene solución la función no corta al eje OX, es decir, será siempre positiva o siempre negativa.
5º) Por último, si con todo lo anterior no es suficiente para poder realizar la representación, siempre podemos hacer una tabla de valores, recordad dar valores a ambos lados del vértice.
Además de estos elementos, existen otros aspectos que pueden ser de interés al estudiar las parábolas. Por ejemplo, la dirección de la parábola, que puede ser hacia arriba o hacia abajo, dependiendo del signo del coeficiente a. Si a es positivo, la parábola se abre hacia arriba, mientras que si a es negativo, la parábola se abre hacia abajo.
Otro aspecto interesante es la amplitud de la parábola, que está relacionada con el valor absoluto del coeficiente a. A mayor valor absoluto de a, más «estrecha» será la parábola, y a menor valor absoluto de a, más «ancha» será.
También es importante mencionar el concepto de parábola canónica. Una parábola se dice que está en su forma canónica cuando la ecuación es de la forma y=a(x-h)²+k, donde (h,k) son las coordenadas del vértice. Esta forma de la ecuación nos permite identificar rápidamente el vértice de la parábola y la dirección en la que se abre.
Finalizaremos, como es costumbre, realizando un ejemplo:
Ejemplo: Representar la siguiente función cuadrática:
1º) Como a=-1<0, sabemos que su forma será como la inversa de la U.
2º) Vamos a calcular su vértice, para ello, en primer lugar calculamos la coordenada x, y después sustituimos en la ecuación:
Obtenemos que las coordenadas del vértice son: (2,1)
3º) Su eje de simetría es x=2.
4º) vamos a calcular ahora los puntos de corte:
-Puntos de corte con el eje OY: Sustituyendo en la ecuación por x=0, obtenemos que y=-3, entonces mi punto de corte es: (0,-3)
-Puntos de corte con el eje OX: Como y=0, resolvemos la ecuación de segundo grado y obtenemos dos soluciones: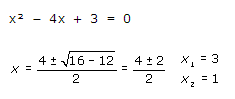
Por tanto los puntos de corte son: (1,0) y (3,0)
5º) Representamos en los ejes los puntos característicos obtenidos y unimos obteniendo nuestra parábola:
Esperamos que este artículo te sea de utilidad para entender las parábolas y sus características. Recuerda que la práctica es esencial para dominar estos conceptos, así que te animamos a que practiques con diferentes ejemplos de funciones cuadráticas y sus gráficas.