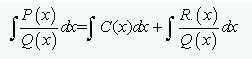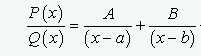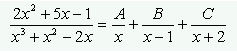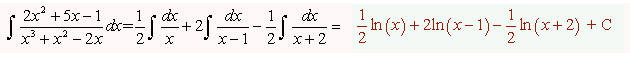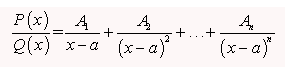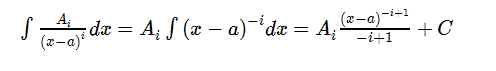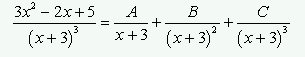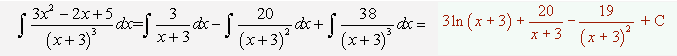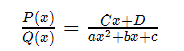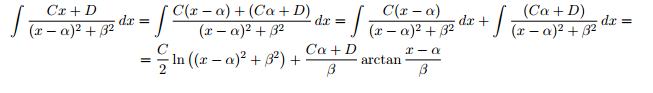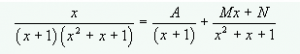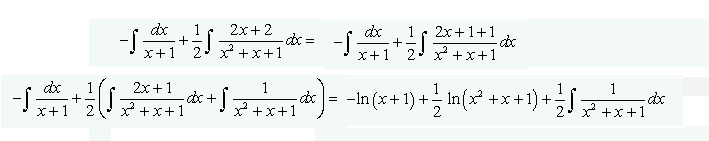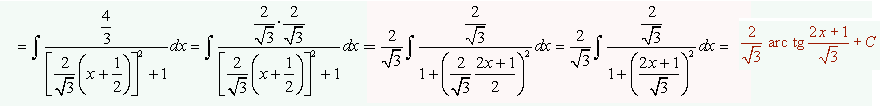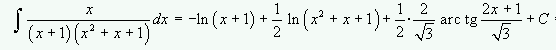Integrales racionales
En el artículo de hoy vamos a aprender a resolver integrales racionales, es decir, cuando tenemos que integrar P(x)/Q(x). Por tanto distinguiremos en varios casos, dependiendo de, en primer lugar: de los grados de los polinomios, y a continuación dependiendo del carácter de Q(x).
CASO A: Si el grado P(x)≥grado Q(x)
Cuando nos encontremos en esta situación tenemos que realizar la división polinómica, obteniendo un cociente C(x) y un resto r(x), de la siguiente manera:
Por tanto, la integral que tenemos que resolver se transforma en esta otra. Donde la primera integral de C(x), es inmediata, puesto que se trata de un polinomio. Y la segunda integral se convierte en una integral del Caso B, ya que el grado del numerador es menor que el del denominador.
CASO B: Si el grado P(x)<grado Q(x)
Cuando nos encontramos este caso, lo primero que tenemos que hacer es factorizar o intentar factorizar el denominar. Lo cual nos lleva a que también nos podemos encontrar con situaciones diferentes dependiendo del carácter de las raíces de Q(x), ya sean simples, múltiples o complejas.
CASO B.1- Si Q(x) tiene raíces reales y distintas.
Supongamos que Q(x) tiene dos raíces a y b, por tanto separamos nuestro cociente inicial en la suma de dos nuevos cocientes con denominadores (x-a) y (x-b) respectivamente.
Como podemos ver, por numeradores tendrán dos números reales A y B, que obtendremos igualando los denominadores una vez hecho el mínimo común múltiplo, es decir, tendríamos que hallar el valor de A y B a partir de la siguiente expresión: P(x)=A(x-b)+B(x-a).
Finalmente, resolveríamos las dos integrales que nos han quedado, las cuales son del tipo logaritmo neperiano.
Ejemplo: Resolver la siguiente integral: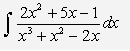
Como se trata de una integral racional donde el grado del numerador es menos que el denominador, factorizamos el denominador y obtenemos:
Donde A=1/2, B=2 y C=-1/2.
Por tanto, la integral que tenemos que resolver se ha transformado en esta otra de resolución sencilla:
CASO B.2- Si Q(x) tiene raíces múltiples.
Supongamos en este caso, que Q(x) tiene una única raíz de multiplicidad n. Por tanto, el cociente inicial lo separemos de la siguiente forma:
Donde los coeficientes A1, A2,…..An, son números reales, que hallaremos dando valores a x y resolviendo el sistema, o bien, desarrollando las expresiones e igualando coeficientes (ambos métodos se pueden utilizar en todos los casos).
Cada una de estas integrales ya son inmediatas, la primera es de logaritmo neperiano, mientras que las siguientes serían integrales de potencias negativas:
Cuando haya tanto raíces simples como múltiples se procede de la misma manera, teniendo en cuenta que para las múltiples habrá tantas fracciones como su multiplicidad.
Ejemplo: Resolver la siguiente integral:
A simple vista podemos ver que Q(x) tiene -3 como raíz múltiple con multiplicidad 3. Por tanto el cociente inicial se expresaría de la siguiente manera.
Donde obtenemos que A=3, B=-20 y C=38.
Por tanto la integral que tenemos que resolver sería la siguiente:
CASO B.3- Si Q(x) tiene raíces complejas.
El último caso, así como el más complicado, es cuando nuestro denominador no tiene raíces reales. En este caso, normalmente, nos quedará una integral con logaritmo neperiano y otra integral de arcotangente; pudiendo ser en algunas ocasiones únicamente una arcotangente cuando el numerador sea un número entero y no un polinomio de primer grado.
Por tanto, cuando Q(x) es un polinomio de segundo grado con raíces complejas, nuestro cociente se descompondría de la siguiente forma:
Para poder continuar, tenemos que convertir Q(x) en un binomio al cuadrado, tal que:
Ejemplo: Resolver la siguiente integral: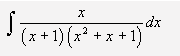
Como uno de los factores no tiene raíces reales, el cociente inicial se convierte en el siguiente:
Donde A=-1, y M=N=1.
Por tanto nos quedan la siguientes integrales, que tenemos que ir transformando.
Por último para resolver la última integral:
Finalmente el resultado es: