Integrales elípticas
La integración es un concepto elemental en ciencias matemáticas, principalemtne en la rama del cálculo y del análisis. De forma simple podemos decir que una integral es la suma de infinitos sumandos, que son a la vez infinitamente pequeños. Entonces una integral elíptica corresponde a una integral de la forma siguiente :
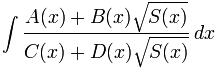
o de otra forma :
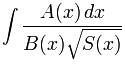
Aquí, A, B, C y D representan polinomios en x y S representa un polinomio de grado 3 ó 4.
La evaluación de integral elíptica tiene inicio en problemas que se relacionan con el cálculo de la longitud de segmentos elípticos. Podemos referirnos a una integral elíptica como la generalización de una función trigonométrica inversa, también pueden llegar a proporcionar la solución para problemas de cálculo como por ejemplo la medida del arco de una circunferencia.
Podemos reescribir las integrales elípticas en forma de adición de funciones elementales. Podemos nombrar tres clases «básicas» de estas integrales. La primera clase a la cual haremos referencia son las integrales elípticas de primera especie, se pueden subdividir en completas e incompletas. Las primeras completas son dependendientes de una única variable y las incompletas dependen de dos variables.
•Integrales elípticas de primera especie
Se pueden definir como:
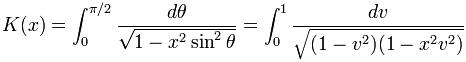
Se calcula mediante la media aritmética geométrica, o también por medio de la serie de Taylor:
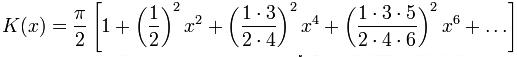
La anterior serie es convergente para,
![]()
Este método posee una interesante pecualiaridad, ya que genera una serie que converge de manera vertiginosa. Si se quiere proceder a la aplicación de esto, basta con inicializar el algoritmo de la media aritmética geométrica con los valores que vemos a continuación:
![]()
K(x) es obtenido a partir del infinito valor an, entonces:
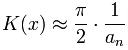
Habitualmente es suficiente si se computan los 5 ó 6 términos iniciales que corresponden a la serie para luego llegar a una gran precisión en el resultante. Lograr lo dicho anteriormente con la serie de Taylor, requiere del cálculo de un número superior, según |x| se aproxima a 1.
La integral elíptica incompleta de primera especie F se define de la siguiente forma:
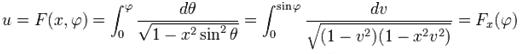
En este caso, el siguiente parámetro,
![]()
es denominado «amplitud» y si tomamos x como parámetro, la «amplitud» será el resultado de la inversa de la función anterior F. Las funciones elípticas de Jacobi pueden ser definidas partiendo de la amplitud.
• Integrales elípticas de segunda especie
Podemos definir a la integral elíptica completa de segunda especie E como:
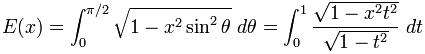
Decimos que es la función de una variable que puede llegar a expresarse en serie de Taylor:
![]()
La integral elíptica incompleta de segunda especie corresponde a una función de dos variables la cual puede generalizar a la integral completa:
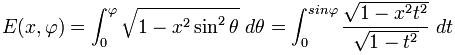
• Integral elíptica de tercera especie
Sea 0 < k2 < 1, la integral elíptica completa de tercera especie se define como:
![]()
donde n corresponde a una constante.
Estas integrales aparecen de manera natural cuando se integran las ecuaciones de movimientos de péndulos esféricos.
Además de las aplicaciones ya mencionadas, las integrales elípticas también tienen una amplia gama de aplicaciones en física y en ingeniería. Por ejemplo, en la teoría de la elasticidad, las integrales elípticas se utilizan para resolver problemas de deformación de cuerpos elásticos. En la teoría de la electricidad y el magnetismo, las integrales elípticas aparecen en el cálculo de la capacidad de los condensadores y en la resolución de problemas de propagación de ondas electromagnéticas.
En la teoría de la relatividad, las integrales elípticas se utilizan para calcular la trayectoria de las partículas en campos gravitatorios. En la teoría cuántica de campos, las integrales elípticas aparecen en el cálculo de las amplitudes de dispersión.
En la teoría de las ondas de choque, las integrales elípticas se utilizan para calcular la forma de las ondas de choque. En la teoría de la hidrodinámica, las integrales elípticas se utilizan para resolver problemas de flujo de fluidos.
En la teoría de la acústica, las integrales elípticas se utilizan para calcular la propagación de las ondas sonoras. En la teoría de la óptica, las integrales elípticas se utilizan para calcular la propagación de las ondas de luz.
En resumen, las integrales elípticas son una herramienta matemática muy útil y versátil que tiene una amplia gama de aplicaciones en muchas áreas de la física y la ingeniería.
