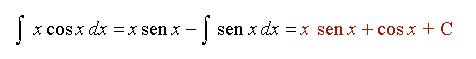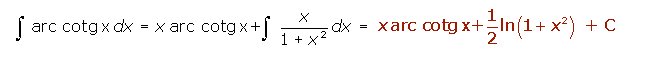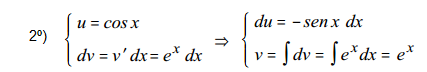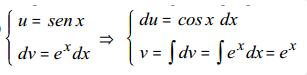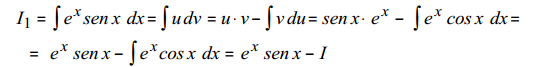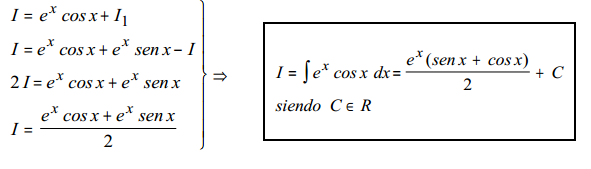Integral por partes

Vamos a ver un nuevo método para poder resolver las integrales que no son inmediatas ni integrales racionales. Se trata de integrales en las que aparecen las siguientes funciones:

A_ Funciones arco: arcoseno, arcocoseno, arcotangen.

L_ Funciones logarítmicas.

P_ Funciones polinómicas.

E_ Funciones exponenciales.

S_ Funciones seno: seno y coseno.

Para recordar esta funciones, vamos a utilizar la primera de letra de cada función obteniendo ALPES.

Cuando tengamos el producto de dos funciones de las del tipo anterior o cuando tengamos una función arco o logarítmica solas, utilizaremos la integración por partes.

La fórmula que nos permite calcular la integral del producto de dos funciones es la siguiente:

Una de las varias reglas nmemotécnica que se utiliza habitualmente es la sigiuente: «fumando un día vi, una vaca menos(–) flaca vestida de uniforme». Como podemos ver, a los símbolos de la integral le asocia una f, aunque el símbolo de la integral realmente hace referencia a la S de superficie, pero bueno, mientras sirva para aprendernos la regla….

Por tanto, llevaremos a cabo los siguientes paso:

1º) Eligiremos un factor del producto al cual llamaremos u y al otro dv. En el caso en el que tenemos una sola función (caso del arco o logaritmo) llamamos u a la función y dv=dx. Para elegir a cual de nuestros factores llamamos u y a cual dv, tendremos que volver a la lista de las funciones, y llamar u a la primera que aparezca en ALPES.

2º) Para poder aplicar la fórmula, al factor que hemos llamado u, lo derivamos, obteniendo du; mientras que al factor que hemos llamado dv, lo integramos, obteniendo v:

u → (derivamos)→ du

dv→ (integramos) → v

3º) Por último sustituimos en la fórmula y resolveremos la siguiente integral. Habrá ocasiones en las que tengamos que volver a aplicar partes. Incluso puede ser que volvamos a la integral inicial.

Veremos algún ejemplo de lo que acabamos de comentar.

Ejemplo 1: Calcular la siguiente integral:

1º) Esta integral es el producto de un polinomio:x, y un función seno: cos x. Por tanto fijándonos en nuestra lista ALPES, llamamos u=x (ya que como hemos mencionado antes es la primera que nos encontramos); y por tanto llamamos dv=cosxdx.

2º) Calculamos du, derivando la función que hemos llamado u, y v, integrando la función que hemos llamado dv de la siguiente manera:

u=x → (derivamos)→ du=1dx

dv=cosdx dx→ (integramos) → v=senx

3º) Sustituimos en la fórmula obteniendo la siguiente expresión, y resolvemos la integral obtenida que es inmediata, ya que se trata de la integral del sen x.

Ejemplo 2: Veamos ahora como resolver una integral que solo tiene un factor:

1º) Como solo tiene un factor, este será nuestra u, u=arccotg x; y por tanto dv=1.

2º) u=arccotg → (derivamos)→ du=x/(1+x^2)

dv=1dv→ (integramos) → v=x

3º) Sustituyendo en la fórmula, obtenemos una integral del tipo de logaritmo neperiano:

Ejemplo 3: Por último, veamos el caso más pesado, cuando haciendo partes dos veces, volvemos a la integral de partida:

1º) En este caso, realmente es indiferente quien sea u y dv. Lo haremos en este caso llamando u=cos x.

3º) Sustituimos y nos queda la integral I1, que en este caso no es inmediata, y tenemos que volver a aplicar partes. Es importante que continuemos llamando de la misma manera a las incógnitas.

4º) Hacemos de nuevo partes en la integral I1, donde llamamos u a la función seno.

Aplicando la fórmula:

5º) Llegamos a la integral inicial:I, por tanto nos planteamos el siguiente sistema y llegamos a la solución final despejando I: