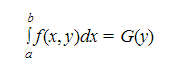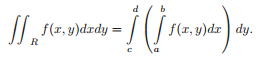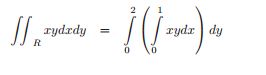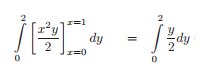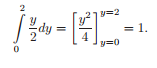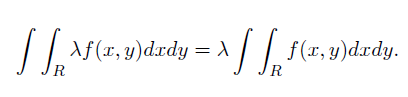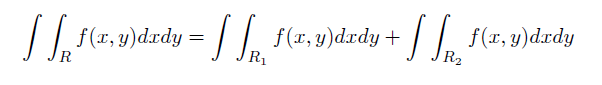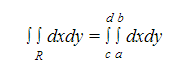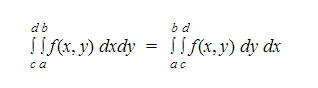Integrales dobles

En anteriores artículos hemos visto distintos métodos de resolución de integrales, así como sus aplicaciones, pero siempre con funciones definidas en una variable. Ha llegado el momento de estudiar las integrales definidas de funciones de dos variables f(x,y) respecto de estas dos variables en un recinto cerrado R. Por tanto, hoy vamos a extender el concepto que teníamos de integral definida de una función en un intervalo cerrado [a,b] al de integral doble definida en el recinto cerrado R=[a,b]x[c,d].

DEFINICIÓN:

Sea f(x,y) una función continua para los valores de x,y que pertenecen a R. Para un y fijo obtenemos la función F(x)=f(x,y) que también es continua y por tanto integrable en [a,b], por tanto:

La función obtenida, G(y), es continua y por tanto integrable en [c,d] de tal forma que podemos definir la integral doble de la función f(x,y) el rectángulo R=[a,b]x[c,d] como:

Es decir, realizar una integral doble consiste en realizar dos integrales simultáneas, una en primer lugar en función de x, considerando que la y es una constante; y en segundo lugar en función de y (en este caso ya no habrá ningún termino con x).

Ejemplo: Calcular la integral doble ∫∫xy dxdy en el rectángulo R= [0,1]x[0,2].

En primer lugar escribimos la integral que nos piden, colocando en su lugar los límites respecto a los cuales tenemos que integrar:

Resolvemos la integral que está en el paréntesis, es decir, la integral respecto de x donde y es una constante:

Por último, el resultado anterior lo integramos respecto de y.

INTERPRETACIÓN

El valor que obtenemos al resolver la integral es un número real que se utiliza para determinar el valor del volumen del sólido situado de forma vertical sobre el rectángulo R del plano OXY bajo la superficie z=f(x,y) siempre y cuando f(x,y)≥0.

PROPIEDADES:

1. Se cumple la propiedad de linealidad:

– Si hay un escalar multiplicando dentro de la integral se puede sacar factor común:

– La integral de la suma de dos funciones dobles f(x,y) + g(x,y) es igual a la suma de la integral doble de cada una de ellas:

2. Cumplen la propiedad de la monotonía:

Si f(x,y)≤g(x,y) para todos los valores de (x,y) pertenecientes a R, entonces ∫∫f(x,y)dxdy ≤ ∫∫g(x,y)dxdy.

3. Si el recinto R se puede dividir en dos recintos disjuntos R1 y R2, es decir, tal que R1 U R2 = R y cuya intersección sea vacía o lo que es lo mismo que R1∩R2 no tenga área, entonces:

4. El área del recinto R=[a,b]x[c,d] se puede calcular mediante la siguiente integral:

5. Podemos intercambiar los límites de integración siempre y cuando cambiamos también el orden de las variables respecto a las que estamos integrando:

6. La función del valor absoluto, |f(x,y)| también es integrable y verifica que:

Recordemos que también podemos realizar integrales dobles sobre recintos que no sean rectángulos, estas integrales se estudian más a fondo en carreras de ciencias como las ingenierías, por tanto, por ahora, este ha sido un buen comienzo.