Función sinc
La función sinc se denota como sinc (x) y posee dos formas de definición. La primera definición a la haremos referencia en la definición normalizada , esta se relaciona con el análisis de sistemas y señales en ingeniería lo cual es importante para el procesamiento de señales digitales (audio, voz, imágenes, video). También se relaciona con la teoría de la información. Esta es una rama matemática que encierra la probabilidad y la estadística y que trata el estudio de la información y su relacionamiento (canales de comunicación, canales de datos, criptografía, compresión de datos, , etc) Generalmente se define de la siguiente forma:
![]()
Además de su importancia en el procesamiento de señales digitales y la teoría de la información, la función sinc también juega un papel crucial en la teoría de la comunicación. En particular, es esencial en la modulación y demodulación de señales, que son procesos fundamentales en la transmisión de información a través de canales de comunicación. En este contexto, la función sinc se utiliza para modelar el efecto de la modulación y demodulación en la señal transmitida.
La función sinc desnormalizada es utilizada en matemática (funciones de Bessel) y proyecciones cartográficas (Proyección de Winkel-Tripel) Se define de la siguiente forma:
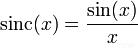
En los dos casos vistos de funciones sinc, los valores de las funciones poseen una singularidad previsible en cero, lo cual habitualmente se determina como una igualdad a 1.
La función sinc es metódica y analítica en todas partes. Surge en el análisis de Fourier así como también en el estudio de sistemas LTI (un sistema LTI, Linear Time-Invariant, o sistema lineal e invariante en el tiempo tiene la característica de cumplir las propiedades de linealidad e invarianza en el tiempo) La función desnormalizada es correspondiente a la normalizada a excepción del factor de escala carente en la explicación. La función sinc equivale también a la transformada de Fourier de un pulso rectangular mientras que la transformada inversa de Fourier de un espectro cuadriforme es correspondiente a una función sinc.
Veamos sus propiedades:
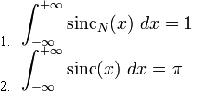
Integral senoidal:
La integral senoidal es una función definida por medio de la integración de la función sinc:
![]()
No es posible que esta integral se pueda expresar como la representación de una función elemental. Por medio de una integración término a término, podemos ver que la integral senoidal puede entonces manifestarse como una serie, veamos:
![]()
Algunas propiedades de la integral senoidal son las siguientes:
• Al ser la integral de una función par, será una función impar, esto es, Si(-x) = -Si(x).
• El valor de Si(x) cuando x tiende a infinito será el límite:
![]()
• De igual forma, el valor de Si(x) cuando x tiende a menos infinito es el que sigue,
![]()
Además, la integral senoidal tiene una serie de propiedades interesantes que la hacen útil en una variedad de aplicaciones. Por ejemplo, es una función de Lipschitz de orden 1, lo que significa que su derivada es acotada. Esto la hace útil en el análisis numérico, donde las funciones de Lipschitz a menudo aparecen en el análisis de la estabilidad de los algoritmos numéricos. Además, la integral senoidal también aparece en la solución de ciertas ecuaciones diferenciales, lo que la hace relevante en campos como la física y la ingeniería.
