Integral de Fresnel

Las integrales de Fresnel, denotadas como S(x) y C(x), son dos funciones trascendentes (no algebraicas), que son empleadas para el cálculo de ondas en física, entre otros campos. Se definen mediante las siguientes expresiones integrales:

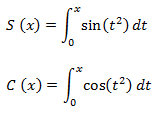
Estas dos integrales se pueden expresar en forma de potencias, que convergen para todo x:

 

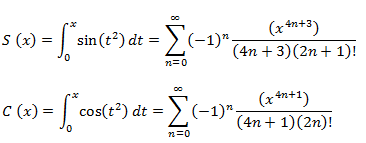
Propiedades:

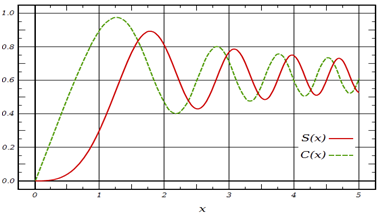
a) C(x) y S(x) son funciones impares de x

b) Se pueden extender al dominio de los números complejos gracias a las expansiones en series de potencias expresadas anteriormente. Obteniendo así funciones analíticas de una variable compleja.

c) Se pueden expresar usando la función error, quedándonos la siguientes expresiones:

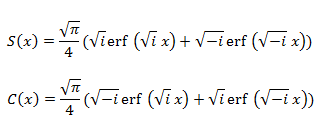
d) No es posible evaluar las integrales que definen S(x) y C(x) en un intervalo cerrado, por lo que los límites de estas funciones, cuando x tiende a infinito son:

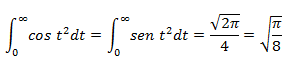
Casos particulares:

S (0)=C (0) = 0

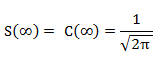
Ejemplo:

>> Resuelve la siguientes integrales de Fresnel:

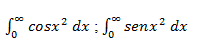
Como función a estudiar vamos a tomar la siguiente:

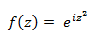
Y cuyo recinto es:

 

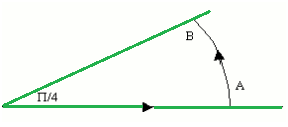
Aplicando el teorema de residuos, y considerando que no encontramos ningún cero en dicho recinto, tenemos que:

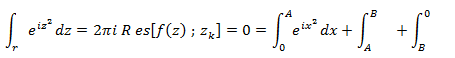
Ahora procedemos a trabajar la segunda integral:

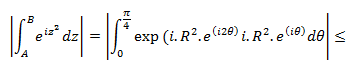
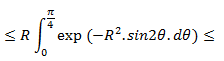
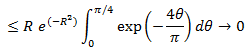
Con lo que nos queda que en AB:

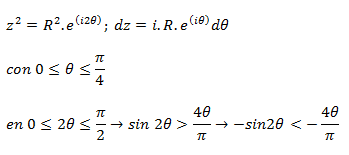
Lo que nos queda por hacer es calcular la última integral, procedemos así:

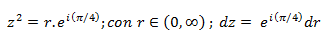
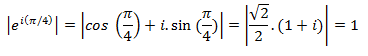
Por tanto:

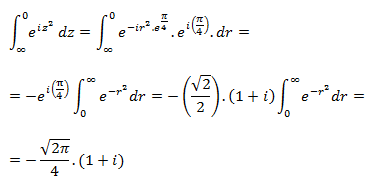
**Nota: En este caso nos aparece una integral de Euler, pero como no es el tema a tratar, simplemente continuaremos resolviendo:

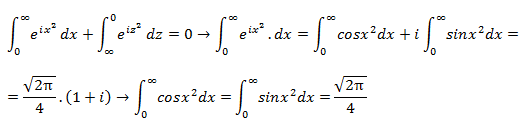
Y así se termina el ejercicio, muchas gracias por su atención.