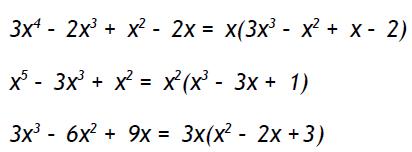Igualdades notables
Llamaremos igualdades notables a algunas identidades que son útiles en general para simplificar expresiones, acelerar cálculos, factorizar o desarrollar expresiones matemáticas. A continuación conoceremos algunas de estas identidades.
El cuadrado de una suma es ciertamente igual al cuadrado del primer sumando más el doble producto del primero por el segundo más el cuadrado del segundo o sea:
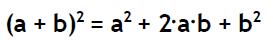
Algunos ejemplos:
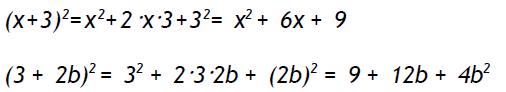
El cuadrado de una diferencia o de una resta sería igual al cuadrado del primero menos el doble producto del primero multiplicado por el segundo sumando luego el cuadrado del segundo. O sea :
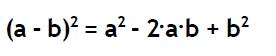
Veamos algunos ejemplos:
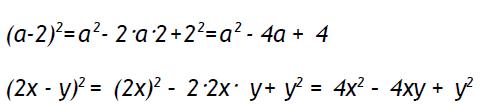
En la diferencia de cuadrados el producto de una suma multiplicado por la diferencia de dos sumandos es igual a la diferencia de sus respectivos cuadrados. O sea:
![]()
Algunos ejemplos:
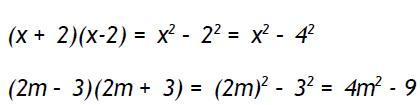
No es recomendable aplicar estas identidades cuando es posible efectuar las operaciones que se encuentran entre paréntesis. Si es así se debe proceder a efectuar primeramente esas operaciones, como muestran los siguientes ejemplos:
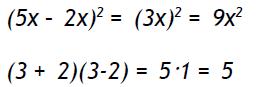
La transformación de sumas en productos, es un modo de convertir expresiones en la que hay presentes sumas o restas en otras en las cuales la operación primordial es un producto. Esto es aplicable únicamente en determinados casos, observemos los siguientes ejemplos:
En caso de transformar un trinomio de segundo grado en el cuadrado de una suma o resta:
![]()
Ejemplos :
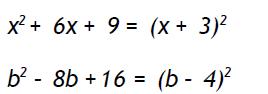
Determinemos también como una diferencia de cuadrado es igual a la suma multiplicada por la diferencia, o sea:
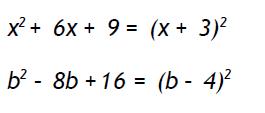
Algunos ejemplos:
Si todos los coeficientes poseen algún divisor común podemos sacar el factor común. También cuando la variable aparece en todos los sumandos. En este caso podemos escribirlo, elevada al exponente de menor valor, como factor común que así multiplica al polinomio con todos los grados restados en sus tantas unidades como tiene el exponente aludido. Observemos los siguientes ejemplos: