Identidad matemática

Una identidad matemática es un tipo de igualdad matemática, entre expresiones algebraicas que se verifica para cualquier valor de alguna variable de todas las que intervienen en la expresión. No es más que el comportamiento de dichas expresiones, como van a reaccionar ante cualquier valor que queramos estudiar, podríamos decir, hablando de modo figurado, que es la «personalidad» que poseen unas expresiones algebraicas concretas.

Un ejemplo sencillo:

ax + bx = x(a+b)

Es una identidad ya que, cualesquiera que sean los valores de a, b y x, la igualdad que escribimos más arriba se cumplirá siempre. Entonces si lo ponemos en números:

a= 1, b=2 y x=3

ax + bx = x (a+b) -> 1.3 + 2.3 = 3 (1+2) -> 3 + 6 = 3.3 -> 9=9

Por tanto, la igualdad se cumple.

Sin daros cuenta habréis visto montones de estas identidades, cuando estudiasteis las funciones algebraicas y sus propiedades (distributiva, conmutativa, asociativa, etc.), aquí simplemente se les da un nombre concreto a este fenómeno.

Además de las identidades algebraicas, también existen las identidades trigonométricas, las identidades exponenciales y logarítmicas, y las identidades hiperbólicas. Cada una de estas categorías tiene su propio conjunto de reglas y propiedades, pero todas comparten la característica común de ser verdaderas para todos los valores de sus variables.

Las identidades matemáticas son herramientas fundamentales en muchas áreas de las matemáticas, incluyendo el álgebra, la trigonometría, el cálculo y la teoría de números. Son esenciales para simplificar ecuaciones y expresiones, y para resolver problemas complejos. Además, las identidades matemáticas a menudo revelan relaciones profundas y sorprendentes entre diferentes áreas de las matemáticas.

Voy a poner unos cuantos ejemplos más para que podáis observar que siempre es lo mismo, lo único que va a ir cambiando son las expresiones, pero el concepto es común para todas ellas: constantemente se cumplen lo que recen ambos lados de la igualdad. Tienen como función primordial hacer más sencilla una expresión que, de otra forma, nos resultaría compleja.

>>Ejemplos:

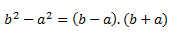
Así podemos saber, que la suma por diferencia de los binomios, es la diferencia al cuadrado de los términos b y a, sin necesidad de ir multiplicando uno por uno.

Resolvamos lo de arriba sin saber que es una identidad:

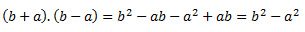
De esta forma, aunque es correcta, perdemos un valioso tiempo que ahorraríamos de conocer esa identidad, vamos, que pensad en los pobres matemáticos que se rompieron el coco para que vosotros conocieseis estas identidades, que no se diga que fue en vano.

Además, las identidades matemáticas también juegan un papel crucial en la física, la ingeniería y otras ciencias aplicadas. Por ejemplo, las identidades trigonométricas se utilizan en la física para describir las oscilaciones, las ondas y la rotación. Las identidades exponenciales y logarítmicas son fundamentales en la teoría de la información, la teoría de la señal y la teoría de la probabilidad.

Bromas aparte, no debemos olvidarnos de las identidades trigonométricas (las que usan senos y cosenos), que es más de lo mismo pero referido a ángulos. Os dejo un par de ejemplos abajo:

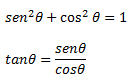
Estas incluso son más útiles, pues nos quitan de hacer engorrosos cálculos. No voy a decir de donde salen, pues para ello ya tenemos un tema referido a esto.

Lo que sí os voy a explicar es lo siguiente, estamos de acuerdo en que, para que una identidad se cumpla, ha de cumplirse la igualdad planteada para cualquier valor, pero ¿Qué sucedería si, para un cierto valor, esa igualdad no se cumpliese? ¿Estaríamos ante una identidad? Retomemos el ejemplo anterior:

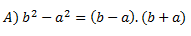
En este caso se cumple siempre, ya que, sean cuales sean los valores de a y b, la diferencia de sus cuadrados siempre va a ser igual a la suma por diferencia.

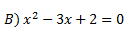
Esto es una ecuación de segundo grado, para ella, encontramos dos soluciones:

x=1 y x=2

Si probamos con cualquier otro valor, por ejemplo 5, pasa lo siguiente:

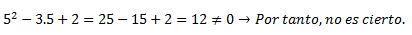
Con x=1 sin embargo:

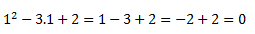
**Pista: Si tenéis dudas de si una solución es correcta, sustituidla en la ecuación, para ver si cumple la igualdad.

Finalmente, es importante recordar que las identidades matemáticas no son solo curiosidades abstractas. Son herramientas poderosas que nos permiten simplificar y resolver problemas, y revelan conexiones profundas entre diferentes áreas de las matemáticas y las ciencias. Por lo tanto, es esencial aprender y entender las identidades matemáticas, y saber cómo y cuándo usarlas.

Aquí me quedo con ésta introducción a las identidades matemáticas, nos vemos en otro artículo de laguia2000.