Identidades Notables

Las identidades notables son varias expresiones algebraicas que por su utilidad conviene conocer, ya que nos pueden ahorrar mucho tiempo en operaciones laboriosas. A continuación intentaremos definirlas y explicarlas detenidamente una a una.

a) Binomio al cuadrado.

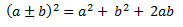
–El cuadrado del primero mas el cuadrado del segundo, más dos veces el primero por el segundo.

Es importante recordar que el binomio al cuadrado es una identidad notable que se utiliza con frecuencia en la resolución de ecuaciones cuadráticas y en la simplificación de expresiones algebraicas. Su comprensión y aplicación correcta puede ahorrar mucho tiempo y esfuerzo en cálculos matemáticos.

b) Suma por diferencia

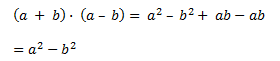
-Aquí es más sencillo, suma por diferencia, diferencia de cuadrados.

Esta identidad notable es especialmente útil cuando se trabaja con polinomios y se busca simplificar expresiones complejas. Es una herramienta valiosa en el álgebra y se utiliza con frecuencia en la factorización y la resolución de ecuaciones.

c) Binomio al cubo

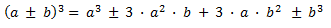
El binomio al cubo es otra identidad notable que se utiliza con frecuencia en el álgebra. Es una extensión del binomio al cuadrado y requiere un poco más de cálculo, pero una vez que se comprende, puede ser una herramienta muy útil para simplificar expresiones algebraicas y resolver ecuaciones.

d) Trinomio al cuadrado

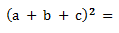
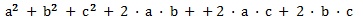
Elevamos los coeficientes al cuadrado y después multiplicamos el doble del primero por los dos restantes y después hacemos el doble del segundo por el tercero.

El trinomio al cuadrado es una identidad notable que se utiliza con frecuencia en la resolución de ecuaciones cuadráticas y en la simplificación de expresiones algebraicas. Es un poco más complejo que el binomio al cuadrado, pero una vez que se comprende, puede ser una herramienta muy útil.

e)Suma de cubos

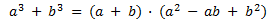
f) Diferencia de cubos

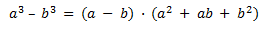
Las identidades de suma y diferencia de cubos son útiles para simplificar y resolver ecuaciones que involucran cubos. Aunque pueden parecer complicadas al principio, con un poco de práctica se vuelven más fáciles de usar.

g) Producto de dos binomios que tienen un término común.

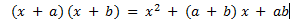
Esta identidad notable es útil cuando se trabaja con binomios que tienen un término en común. Ayuda a simplificar la expresión y a hacer los cálculos más manejables.

Ahora que ya sabemos unas cuantas identidades, pasemos a ver unos ejemplos para comprender su utilidad:

Pensemos en un producto tal que así:

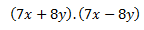
Entonces, si procedemos a su solución paso a paso, sin tener ni idea de identidades nos sale esto:

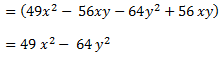
Como veis, son dos líneas que hemos tenido que realizar para resolver algo que simplemente lleva una línea, pues si nos acordamos de la regla: suma por diferencia, diferencia de cuadrados, sabemos que lo único que tenemos que hacer es elevar al cuadrado los términos de la ecuación, en este caso, 7x y 8y y expresarlos en forma de diferencia.

Hagamos otro ejemplo más, pero esta vez lo haremos de la forma inversa, pensemos en un cociente que tiene varias expresiones algebraicas y queremos simplificarlo:

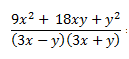
Necesitamos obtener en el numerador o bien 3x – y o 3x + y para poder simplificar el cociente. Si miramos detenidamente encontramos una identidad notable en el numerador, de forma que recordamos el binomio al cuadrado y lo ponemos de forma sencilla arriba:

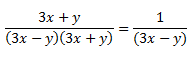
Hemos obtenido por tanto el resultado simplificado que buscábamos gracias a las identidades ¿ A qué son útiles? ¡Nos ahorran un montón de pasos!

Además de las identidades notables que hemos discutido, existen muchas otras que se utilizan en diferentes campos de las matemáticas. Algunas de estas identidades se utilizan en trigonometría, cálculo, geometría y otras áreas de las matemáticas. Cada una de estas identidades tiene su propio conjunto de reglas y aplicaciones, y aprender a utilizarlas correctamente puede ser de gran ayuda para resolver problemas matemáticos complejos.

Bueno, eso es todo, solamente indicaros que las más utilizadas son las dos primeras identidades, así que si no queréis aprenderos todas, por lo menos quedaros con esas.