Cuadrado de una diferencia

Los productos notables cumplen con ciertas reglas determinadas cuyo resultado puede escribirse sin verificar la multiplicación. Las letras representan números reales por lo que se pueden aplicar las propiedades operatorias de los números reales para comprobar la eficacia de cada fórmula. Veamos entonces que sería el cuadrado de una diferencia.

Producto de la suma por la diferencia

Siendo el producto:

(a+b). (a-b)

Se desarrollará esta multiplicación quedando de la siguiente forma:

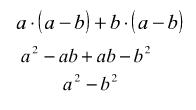
Entonces:

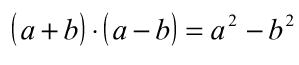
Diremos entonces que la suma de dos valores multiplicado por su diferencia es igual al cuadrado de minuendo menos el cuadrado del sustraendo. El producto de la suma por la diferencia de dos cantidades puede ser representado en forma geométrica cuando sus valores son positivos, veamos la siguiente representación:

En principio tenemos un cuadrado de lado a como el siguiente:

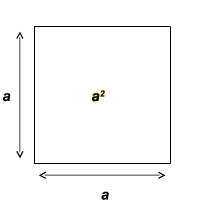
Tenemos construido también un cuadrado de lado b:

Se le quita al cuadrado de lado a el cuadrado de lado b, y se trazan líneas de punto para lograr

obtener así dos rectángulos cuyos lados son b y (a-b) :

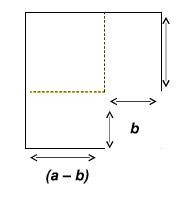
En el ejemplo siguiente se trasladará uno de los rectángulos en la forma que indica la flecha de color amarillo, para luego obtener un rectángulo cuyos lados sean (a+ b ) y ( a –b ):

El área de este rectángulo será entonces:

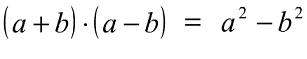
Entonces de esta forma se comprueba que el producto de la suma por la diferencia es una diferencia de cuadrados. Para aclarar mejor el tema podemos decir también que el cuadrado de la diferencia de dos términos es igual al cuadrado del primer término menos el doble producto de ambos términos más el cuadrado del segundo término. Por ejemplo:

para la diferencia de cuadrados debemos tener en cuenta que un binomio es invariablemente una diferencia de cuadrados siempre y cuando los términos de los cuales esté compuesto tengan signos y sus términos tengan una raíz cuadrada exacta.