Geometría del triángulo

Vamos a estudiar los elementos característicos de un triángulo: las rectas notables y los puntos que determinan:

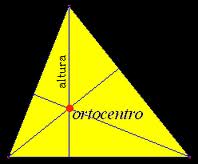
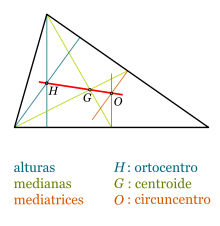
– Se llama altura de un lado de un triángulo a la recta que une cada vértice con el lado opuesto de forma perpendicular. Las tres alturas de un triángulo se cortan en un punto denominado ortocentro.

Propiedad 1:

La altura de un triángulo puede ser tanto interior al triángulo, como se puede apreciar en la imagen; exterior al triángulo; o incluso que coincida con alguno de sus lados. La situación de la altura depende del tipo de triángulo que sea:

a) Si se trata de un triángulo rectángulo, dos de sus alturas coinciden con los catetos, mientras que la altura respecto sobre la hipotenusa es interior.

b) En el caso de los triángulos acutángulos las tres alturas son interiores.

c) Por último, si el triángulo es obtusángulo, la altura correspondiente al lado mayor es interior; en cambio, las otras dos son exteriores.

Propiedad 2: En los triángulos isósceles, la altura sobre el lado desigual divide al triángulo en dos triángulos rectángulos iguales.

Además, es importante destacar que las alturas de un triángulo tienen una relación directa con el área del mismo. La fórmula para calcular el área de un triángulo es la mitad del producto de la longitud de la base por la altura correspondiente. Esto significa que, si conocemos la longitud de la base y la altura de un triángulo, podemos calcular su área.

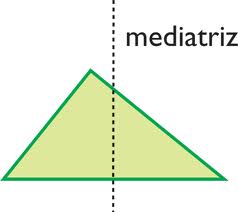
– Se llama mediatriz de un lado de un triángulo a la recta que perpendicular a ese lado que pasa por su el punto medio de dicho segmento. El punto donde se cortan las tres mediatrices se denomina circuncentro. Este punto es el centro de la circunferencia circunscrita al triángulo.

Propiedad: Los puntos de la mediatriz de un lado se encuentran a la misma distancia de los vértices de dicho lado.

Además, es interesante notar que la mediatriz de un lado de un triángulo es también la perpendicular al segmento que une el circuncentro con el vértice opuesto a dicho lado. Esto significa que el circuncentro, el punto medio de un lado y el vértice opuesto están alineados.

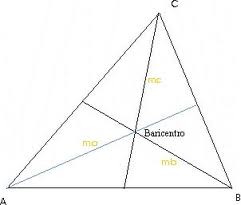
– Se llama mediana de un triángulo a cada una de las rectas que une cada vértice con el punto medio del lado opuesto. El punto donde se unen todos las medianas se denomina baricentro.

Propiedad 1: Las medianas de un triángulo son siempre interiores sin tener en cuenta el tipo de triángulo que se trata.

Propiedad 2: Cada una de las medianas del triángulo divide al triángulos en dos triángulos de igual área.

Además, el baricentro de un triángulo tiene una propiedad muy interesante: es el centro de gravedad del triángulo. Esto significa que si se dibuja un triángulo en una hoja de papel y se recorta, la hoja se equilibrará perfectamente si se coloca en el baricentro.

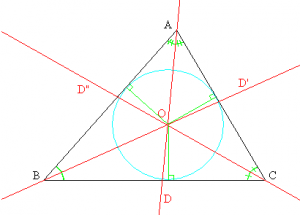
– Se llama bisectriz de un ángulo de un triángulo, a la recta que divide dicho ángulo en dos ángulos iguales. Las bisectrices de un triángulo tienen un punto en común que se denomina incentro. Este punto es el centro de la circunferencia inscrita en el triángulo como podemos apreciar en la siguiente imagen:

Propiedad 1: Los puntos de la bisectriz se encuentran a la misma distancia de los lados que forman el ángulo. O lo que es lo mismo, que si trazamos rectas perpendiculares desde un punto a ambos lados del triángulo, los segmentos tienen la misma longitud.

Propiedad 2: En el caso del triángulo isósceles, la bisectriz del ángulo determinada por los lados iguales, coincide con la altura, la mediana y la mediatriz del vértice que determina el lado opuesto.

Además, es importante mencionar que la bisectriz de un ángulo de un triángulo es también la recta que une el incentro con el vértice del ángulo. Esto significa que el incentro, el punto medio del arco del ángulo y el vértice del ángulo están alineados.

RECTA DE EULER

La recta de la que forman parte el ortocentro, el circuncentro y el baricentro se denomina la recta de Euler, ya que fue el famoso matemático Leonhard Euler quien la descubrió a mediados del siglo XVII.

Además, es importante destacar que la recta de Euler tiene una propiedad muy interesante: la distancia entre el ortocentro y el circuncentro es dos veces la distancia entre el circuncentro y el baricentro. Esta propiedad es válida para cualquier tipo de triángulo, ya sea rectángulo, acutángulo u obtusángulo.