Triángulo de Pascal
El triángulo de Tartaglia también se conoce como triángulo de Pascal ( se de nomina de esta forma en honor a Blaise Pascal, matemático, físico, filósofo y teólogo francés) en las ciencias matemáticas el triángulo de Pascal es un conjunto infinito de números enteros que se encuentran ordenadaos en forma triagular, allí están expresados los coeficientes binomiales. Estos coeficientes corresponden a un serie de números estudiados en combinatoria. Se encargan de indicar la cantidad de formas en que pueden ser extraídos subconjuntos partiendo de un conjunto determinado.
En China, India o Persia, el triángulo de Pascal es mejor conocido como Triángulo de Yanghui, en honor al matemático Yang Hui, quien fue el primero en describirlo en el año 1303. Se encuentra también en la tapa del libro de Chu Shi-Chieh «Ssu Yuan Yü Chien» (Espejo precioso de los cuatro elementos) hace casi setesientos años, aunque en el libro dice que el triángulo ya era conocido mas de dos siglos antes. Fue tema de estudio de matemáticos como Al-Karaji, cinco siglos antes de que Pascal llegara a exponer sus aplicaciones y también por el astrónomo y poeta persa Omar Jayyam (1048-1123).
• Para crear este particular triángulo, debemos en primer lugar colocar un «1» arriba, y luego proseguir a escribir números debajo de forma que se constituya el un triángulo. Cada número corresponde a la suma de los dos números que tiene encima, menos los extremos, lo cual dará siempre «1». Veamos como nos queda:
(Aquí está remarcado que 1+3 = 4)
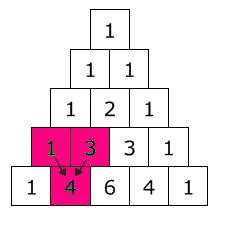
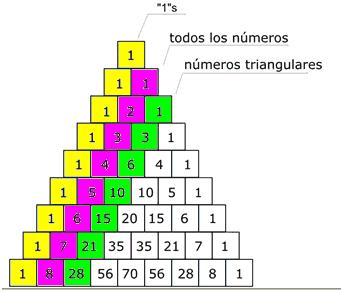
• La primera diagonal está constituida sólo por «unos», y la siguiente posee todos los números consecutivamente (1,2,3, etc.) La tercera diagonal es correspondiente a los números triangulares (aquellos que pueden recomponerse en la forma de un triángulo equilátero) La cuarta diagonal, que no ha sido remarcada, corresponde a los números tetraédricos. Un número de este tipo se denomina también, número piramidal triangular y se trata de un número figurado que simboliza una pirámide de base triangular y tres lados, lo cual se denomina tetraedro. A su vez, un tetraedro es un poliedro de cuatro caras .
• Si los números se adicionan de forma horizontal, se obtendrán las potencias de 2, como se puede observar a continuación:
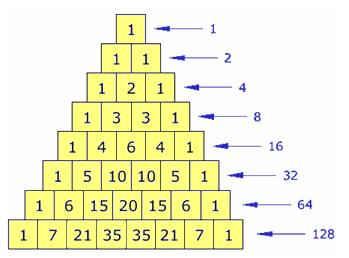
• El triángulo es simétrico, o sea que se ve igual desde la derecha que desde la izquierda
• Como ya sabemos, el número superior es un 1. La segunda fila es correspondiente a los números combinatorios de 1, mientras que la tercera de 2, la cuarta de 3 y así sucesivamente. Los números combinatorios son utilizados para poder establecer grupos en los cuales no importa el orden y los elementos no pueden ser repetidos, es decir, para calcular directamente las combinaciones. Como el triángulo de Pascal permite calcular de una forma sencilla los números combinatorios, es muy útil para calcular los coeficientes del binomio de Newton.
