Arcos compuestos

Volvemos esta vez en la guía matemática con las identidades trigonométricas. Esta vez, daremos los arcos compuestos.

Estas identidades, se conocen como auxiliares, pues nos ayudan a resolver problemas trigonométricos, descomponiéndolos en formas trigonométricas más simples, que nos facilitarán la tarea.

Vamos a mostrar aquí las principales que se usan:

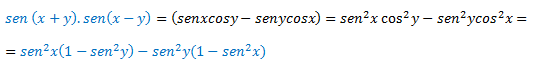
Lo que está en azul es lo que tenéis que memorizar, aunque basta decir que para los pasos previos hemos utilizado identidades para poder resolver ese producto (mirar en esta misma web para encontrarlas).

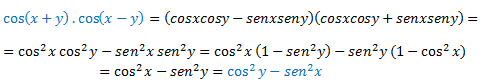
En la formula anteriormente descrita, un truquillo, vemos que, se trata de una suma por una diferencia, por tanto, nos acordamos que es igual a una diferencia de cuadrados. Como es lógico, no es exactamente igual, ya que tenemos al final un seno y un coseno al cuadrado, pero así ya nos acordamos más fácil.

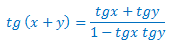
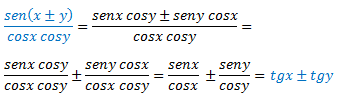
La siguiente formula es casi igual a la anterior, si os fijáis, al principio los numeradores son exactamente iguales, y los denominadores son senos.

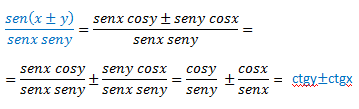
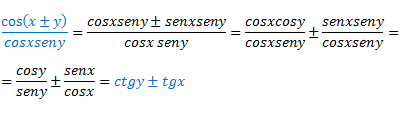
**Nota**: En los casos de los cocientes, se han expuesto dos identidades en una misma fórmula, gracias a la combinación del doble signo más /menos, es decir, por ejemplo, en esta última identidad, si quisiésemos hacer cos(x+y) tendríamos que usar los +, mientras que si quisiésemos aplicar la resta, utilizaríamos el signo negativo.

>>Ejemplo:

Reducir la siguiente ecuación lo máximo posible:

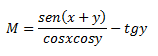
Lo que aquí debemos hacer es aplicar las identidades antes mencionadas, en este caso, vemos ese sen(x+y) . Queda, una vez sustituido:

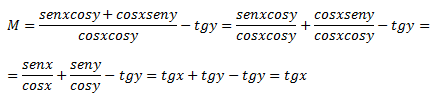
Como observamos, el resultado final es tgx.

Para todos los demás ejercicios, deberéis proceder de igual manera, sustituyendo cuando podáis por las formulas antes descritas.

¡¡Nos leemos en la siguiente lección!!