Forma cuadrática

En matemáticas, una forma cuadrática se relaciona con un polinomio homogéneo de grado dos en un número de variables. Para introducir mejor el concepto de forma cuadrática comenzaremos viendo lo que son los polinomios cuadráticos. Diremos que un polinomio p en las variables x1,x2,…,xn es cuadrático, si cada uno de sus términos posee grado dos, o sea :

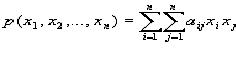
siendo aijðR, i,j=1,…,n los coeficientes del polinomio y las variables xi, i=1,…,n

Teniendo claro el concepto de polinomio cuadrático, en un conjunto de variables, también podríamos explicarlo como una aplicación tal que a cada vector n-dimensional (x1,x2,…,xn) de Rn se le asocia el número real p(x). A continuación veamos el concepto de Forma cuadrática. Una forma cuadrática es toda aquella aplicación de Rn en R tal que a cada vector (x1,…,xn)ð Rn le hace relacionar el valor numérico dado por un polinomio cuadrático. Hay tres tipos de expresión de formas cuadráticas, la forma polinómica, la forma canónica y la forma matricial.

Analizaremos a continuación lo que sería una forma canoníca de una forma cuadrática:

Consideremos la siguiente forma cuadrática:

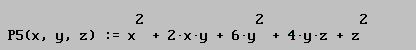
¿será posible expresar esta forma cuadrática como la suma de cuadrados de 3 nuevas variables?

Vamos a suponer que llamamos a las variables :

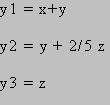
Veamos qué cambios es necesario realizar con las variables x, y, z

Considerando las ecuaciones anteriores .

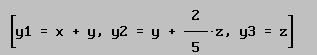
Si procedemos a resolver este sistema respecto de las variables x, y, z obtenemos entonces:

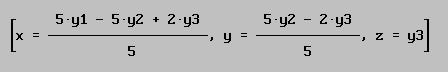
Pero si ahora sustituimos en la expresión que define la forma cuadrática P5 x,y,z por los valores anteriores tendremos:

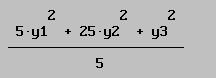
Con este cambio de variables hemos obtenido una nueva forma de expresión de la misma forma cuadrática que ahora asume un aspecto diferente:

El proceso de obtención del cambio de variables podría haber sido de la siguiente forma:

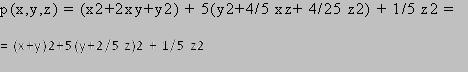
Llamamos forma canónica a este nuevo aspecto y lo definimos de la siguiente forma:

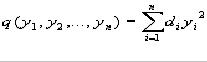
con diðR,i=1,…,n.

Cualquier forma cuadrática se puede expresar siempre en forma canónica.

Ahora volvamos con la forma cuadrática anterior.

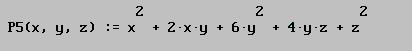
Consideremos la siguiente matriz.

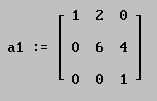
O sea que se obtiene el polinomio cuadrático que define la forma cuadrática. Esta expresión de la forma cuadrática depende de una cierta matriz. Aunque no se ha tenido en cuenta si el vector de incógnitas era fila o columna, ha de observarse que la forma matricial ejecuta el producto de un vector fila por una matriz por un vector columna. la definición de una forma matricial de una forma cuadrática es la siguiente:

Sea q una forma cuadrática en las variables x1,x2,…,xn

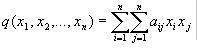
Se puede expresar entonces en forma matricial como

Siendo A una matriz de orden n, y A=(aij) i,j=1,…,n

Si continuamos con la forma cuadrática que vimos anteriormente, podemos observar que otra posible forma matricial se da a partir de la matriz :

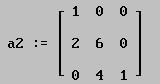
Ya que si efectuamos lo siguiente:

Obtendríamos como resultado la misma expresión polinómica.