Suma de Polinomios

2 de abril de 2010 Publicado por Eduardo

Hola de nuevo, en esta ocasión voy a intentar explicaros que lo que es una suma de polinomios de grado n de una forma sencilla.

Seguramente a estas alturas, todos/as ya sabéis lo que es un polinomio….¿No? Bueno, no pasa nada, que para eso estamos:

Un polinomio es una expresión matemática en la cual se engloban constantes y variables, teniendo éstas últimas un exponente determinado (ya sea 0, 1 2, …n). Llamamos constantes a los coeficientes que acompañan a las variables, no pudiendo estos variar su valor (por ello se llaman constantes, porque siempre son lo mismo, como el que va al fútbol a ver a su equipo todos los domingos aunque pierda, se llama constancia, pues esto es más o menos lo mismo). Y no nos olvidemos de las conocidas variables, ya sabéis, las famosas equis, se llaman así porque pueden cambiar de valor, por ejemplo:

A(x)= 4x + 5

Si a x le damos el valor 3: A(3)= 4×3 +5= 12 +5= 17, lo mismo sucede si le damos el valor cero por ejemplo: A(0)= 4×0 +5= 5. Como sé que sois muy observadores, seguramente no hará falta que os diga que las equis se llaman variables porque tienen la habilidad de cambiar de valor a nuestro antojo, dándonos el valor numérico de nuestro polinomio.

Para terminar con la introducción a los polinomios, deciros que el grado n de un polinomio viene dado por el coeficiente que tenga mayor exponente, es decir:

P(x)= a+ b +cx +d sería un polinomio de grado 5, pues es la mayor potencia () que existe en este polinomio.

Muy bien, ahora que sabemos que son los polinomios, sumarlos es cosa sencilla, es como sumar números, vamos a llamar a dos polinomios A(x) y B(x), tal que:

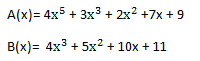
Ahora vamos a sumar A(x) + B(x), de derecha a izquierda, como en las sumas de toda la vida :

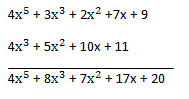
Aquí recordad que no nos «llevamos» nada, es decir, si os da 20, poned 20, hay que sumar cada coeficiente según su grado, dicho de otro modo: los cuadrados con los cuadrados, los cubos con los cubos, y así sucesivamente, ¿Qué no tenéis, como en el ejemplo un coeficiente de igual grado? No pasa nada, dejáis abajo un espacio en blanco como hice yo y sumáis normalmente.

Propiedades de la suma de polinomios:

A) Ley de cierre

La suma de dos o más polinomios nos da otro polinomio

Esto quiere decir que si sumamos A(x) + B(x) el resultado debería de ser otro polinomio C(x), ¿Lógico no?

B) Propiedad asociativa

A(x) +B(x) + C(x) = ( A(x) +B(x) ) + C(x) = A(x) + ( B(x) + C(x) )

C) Elemento neutro

A(x) +0 =0 +A(x) = A(x)

Aquí se nos dice que si le sumas cero a un polinomio, sigue dando cero, con la puntualización de que aquí cero se le llama al polinomio nulo (polinomio formado únicamente por ceros).

D) Propiedad conmutativa

A(x) + B(x) = B(x) + A(x)

Tanto da el orden de los sumandos, el resultado no se altera.

E) Existencia del elemento opuesto

–Si a A(x) le sumas su opuesto –A(x) el resultado es cero

Un ejemplo: -5 es el opuesto a 5, si los sumamos: 5 +(-5) = 0, esto es lo que se pretende demostrar.

Después pasaremos a explicar la resta, que no es más que sumar, pero restando, os parecerá una tontería seguramente, pero sin saber hacer estos cálculos no podréis realizar las divisiones de polinomios más adelante.