Multiplicación de monomios

Primero de todo vamos a ver qué propiedades posee el producto de monomios:

 

a) Conmutativa: Siendo a(x) y b(x) dos monomios cualesquiera de grado n y m respectivamente, se cumple que:

a(x)* b(x) = b(x) * a(x)

b) Asociativa: Si tenemos tres monomios a(x), b(x) y c(x) de distintos grados, se cumple que:

(a(x)*b(x))*c(x) = a(x)*(b(x)*c(x))

c) Elemento neutro: Existencia de un monomio I(x), cuyo valor numérico es uno, y que al multiplicarlo por otro monomio a(x) se cumple:

a(x)*I(x)= a(x)

 

En la multiplicación de monomios, podemos encontrar dos casos posibles:

 

a) Multiplicación de un monomio por un polinomio:

Se trata de efectuar el producto del monomio, por cada uno de los coeficientes y sus variables del polinomio. Veamos un ejemplo:

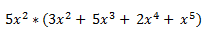
Entonces, procederíamos, con el 5 y la equis a multiplicar ese polinomio:

 

 

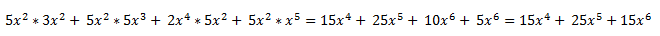
*Pista* : Para multiplicar exponentes de igual base, se pone la misma base y se suman los exponentes.

 

b) Multiplicación de un monomio por otro monomio:

En este caso, procederíamos igual que arriba, multiplicando las potencias de igual base y sumando los exponentes. Ejemplo:

 

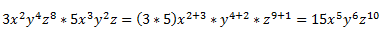
La forma más fácil, es agrupar los coeficientes y luego multiplicarlos por sus variables. Al principio podéis hacerlo así para entenderlo mejor, pero cuando tengáis más práctica es conveniente que los hagáis ya automáticamente sin ese paso previo.

 

c) Multiplicación de un número por un monomio:

Este es el más sencillo de todos, puesto que lo único que debemos hacer es multiplicar los coeficientes por el número, vamos, lo que veníamos haciendo antes pero sin la «complicación» de sumar los exponentes de las variables.

Ejemplo:

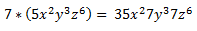
Como observáis, he multiplicado solamente la parte correspondiente al número.

 

Para generalizar, podríamos decir, que un monomio por otro monomio da como resultado, otro monomio cuyos coeficientes son la multiplicación de los coeficientes y cuyas variables se obtienen multiplicando las potencias con la misma base. Esto expresado en fórmula:

 

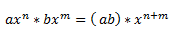
Para acabar con esta lección, recordaros que, al contrario que en la suma de monomios, en la multiplicación no es necesario que sean semejantes, es decir, en el ejemplo del apartado b), los dos monomios no lo eran ya que tenían distintas variables, sin embargo, hemos podido realizar el cálculo, ¿Por qué? Pues sencillamente porque a la hora de multiplicar potencias, lo único que importa es que tengan igual base, lo demás para estos casos no se aplica.

**Pista**: SI en alguna ocasión os encontráis con un producto de monomios tal que haya alguna variable que no se repita, no pasa nada:

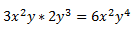
En ese hipotético caso, simplemente la dejáis tal como estaba y multiplicáis los demás coeficientes y variables.