Resta de monomios

En la resta de monomios, de lo que se trata es de realizar una reducción entre monomios semejantes, es decir, con la misma composición de variables, no pudiendo realizarse en caso contrario, siendo el resultado de esta operación, otro monomio. Tendremos que tener mucho cuidado a la hora de mirar los signos, pues toda la cuenta puede salirnos mal si en vez de un menos ponemos un mas.

Diferenciaremos varios casos en la resta de monomios:

 

a) Resta de un monomio con un número entero:

Esto es lo más sencillo que os vais a encontrar en cuanto a restas, pues se trata, al igual que en la suma, de dejar planteada la expresión, ya que, al ser un número entero frente a un monomio, no podemos realizar cálculo alguno. Veamos este sencillo ejemplo:

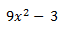
No podemos hacer nada con ese tres, ya que, al no poseer parte literal, no es monomio, por tanto, no podemos operar, simplemente lo dejamos tal cual.

b) Resta de un monomio con un polinomio:

Aquí se complica un poco la cosa, pero aún así es fácil, nada más tenéis que agrupar ese monomio que tenemos con la parte del polinomio que sea semejante, es decir, que tenga dentro de ese polinomio un monomio semejante al de inicio.

Digamos que tenemos esto:

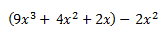
Al observar esta ecuación, vemos que tenemos dos bases iguales, las equis, y que están elevadas a un mismo exponente (el cuadrado). Pues con ese monomio es con el que asociaríamos y efectuaríamos la operación, es decir:

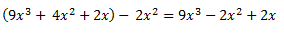
En esta variante, el resultado es un polinomio una vez reducido con nuestro monomio.

 

c) Resta de un monomio con otro monomio:

Bien, esto es muy sencillo, pues es lo mismo que el caso b) pero abreviado a solo dos monomios:

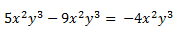
En este segundo ejemplo, no podemos operar de modo ninguno, pues las partes de las variables que acompañan a los coeficientes de los monomios son distintas, en este caso dejaríamos la expresión planteada de la misma forma que se nos ha presentado, formando un polinomio.

 

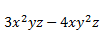
Como todas las operaciones, la resta de monomios tiene unas propiedades que ha de cumplir para poder obtener un resultado:

a) No es una operación interna: Ya que su resultado no tiene por qué ser un monomio, como vimos en el ejemplo, a veces se da el caso de que obtenemos un polinomio al restar dos monomios entre si.

b) No es conmutativa: Ya que, el signo puede variarlo todo. Veámoslo en el siguiente ejemplo:

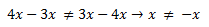
Al cambiar el elemento de posición se produce un cambio en el signo del coeficiente, lo que provoca un resultado distinto. En resumen, hay que fijarse bien a la hora de poner el minuendo y el sustraendo.

**Pista**: Minuendo es la parte que va a ser restada y sustraendo la que se resta, o se «sustrae» , en nuestro ejemplo de arriba sería 4x el minuendo y 3x el sustraendo.

 

Hasta aquí nada más, espero que os haya quedado clara la lección, si tenéis dudas, no os acomplejéis y dejad un comentario y se intentará resolverlas.