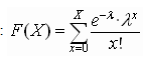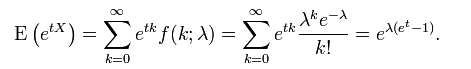Distribución de Poisson

En el artículo de hoy volvemos a retomar la rama de la Estadística para hablar sobre una de las distribuciones discretas más importantes: la distribución de Poisson. Esta distribución se utiliza en situaciones en las que se quiere determinar el número de eventos de un tipo concreto que ocurren en un intervalo de tiempo o espacio dado.

Esta distribución se debe a un matemático y físico francés del siglo XIX, Siméon-Deni Poisson, el cual publicó por primera vez sus estudios sobre la Poisson en su trabajo “Investigación sobre la probabilidad de los juicios en materias criminales y civiles”

PROPIEDADES

1. El campo de variación de la variable, al tratarse de un modelo discreto, es el conjunto de los números naturales, incluido también el cero.

2. Sea x el número de veces que se repite el evento estudiado, y λ un número positivo que nos indica el número de veces que se repite dicho evento durante un intervalo de tiempo o espacio dado; donde λ será nuestro parámetro. Entonces, la función de probabilidad de la distribución de Poisson es:

3. El valor de la media o esperanza y el de la varianza coinciden y son iguales al parámetro λ: E[x]=Var[x]= λ.

4. La función de distribución es:

5. La función generatriz es:

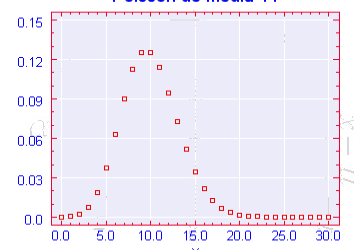
6. La representación en función del parámetro es:

7. La distribución de Poisson cumple la propiedad reproductiva, es decir, podemos sumar dos distribuciones de Poisson de parámetro λ1 y λ2 respectivamente, de tal forma que obtenemos una distribución de Poisson cuyo parámetro será igual a la suma de los anteriores: λ1+ λ2.

RELACIONES CON OTRAS DISTRIBUCIONES

Parte de la importancia de esta distribución se debe a la relación existente con otras distribuciones. Podemos vincularla con las siguientes:

-Distribución binomial: Diremos que una distribución binomial de parámetros n y p, se aproxima a una distribución de Poisson de parámetro λ =np, cuando se cumpla que n>30, p< 0,1 y np<10.

-Distribución normal: Por el Teorema Central del Límite, tenemos que una distribución de Poisson de parámetro λ, tiende a una distribución normal donde la media es λ, y la varianza es λ.

-Distribución exponencial: Cuando el número de eventos de un fenómeno estudiado sigue una distribución de Poisson, entonces los tiempos discurridos entre dos eventos seguidos diremos que sigue una distribución exponencial.

APLICACIONES

Esta distribución puede ser encontrada en varias ocasiones de la vida cotidiana, sobre todo en fenómenos relacionados con la naturaleza, es decir, con los fenómenos que se dan 0, 1, 2….veces en un intervalo de tiempo o espacio. Algunos ejemplos de estos fenómenos que podemos modelar con una distribución de Poisson son:

– El número de peces muertos encontrados por unidad de superficie en una determinada área.

– El número de vehículos que pasan por un rádar fijo durante un intervalo de tiempo concreto.

– El número de llamadas telefónicas recibidas en una central por minuto.

– El número de inventos llevados a cabo por una persona a lo largo de su carrera.

Y así podríamos continuar de forma infinita….