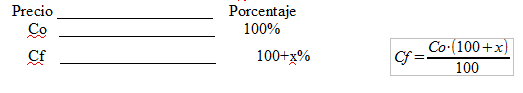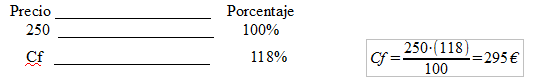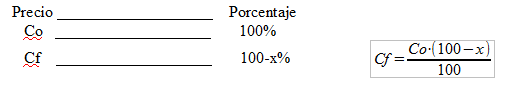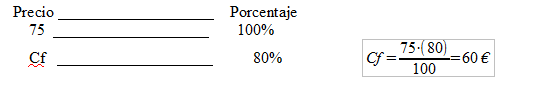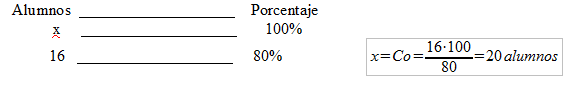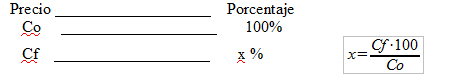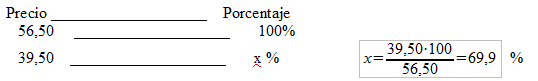Ejercicios con porcentajes

Son muchas las ocasiones de la vida cotidiana en la que nos encontramos con porcentajes: las rebajas, los intereses de un banco, la nota de los exámenes y como no la subida del I.V.A entre otras muchas e innumerables situaciones.

Hoy vamos a ver un ejemplo de aplicaciones de los porcentajes y como resolver los distintos problemas que nos podemos encontrar. También veremos que hay diferentes formas de resolver un problema con porcentajes, una de ellas, la conocida regla de tres.

HALLAR LA CANTIDAD FINAL

El primer caso que vamos a estudiar son los problemas que nos dan la cantidad inicial: Co, nos dicen el porcentaje de subida o bajada; x%, y tenemos que hallar la cantidad final:Cf.

-Formas de resolverlo cuando sube un x%:

1) Podemos calcular la cantidad que se ha subido, y luego sumársela a la cantidad inicial:

Cf=Co +Co*x/100.

2) Utilizando la regla de 3 teniendo en cuenta que cuando hay una subida del x%, significa que el artículo tiene un porcentaje de (100+x)%.

Ejemplo: Un frigorífico tiene un precio en el catálogo de 250€, pero ha ese precio hay que añadirle el 18% de I.V.A. ¿Cuál es el precio final del frigorífico?

1)1ª Forma:

Cf= 250+250*18/100=295€

2) 2ª Forma:

-Formas de resolverlo cuando baja un x%.

1) De forma análoga al caso anterior, podemos calcular el porcentaje de bajada y a continuación restar a la cantidad inicial: Cf=Co-Co*x/100

2) Utilizamos la regla de 3, en este caso tenemos que tener en cuenta que si una cantidad disminuye el x%, quiere decir que la cantidad que nos queda sería (100-x)%.

Ejemplo: Jorge se ha comprado en las rebajas unos pantalones que costaban 75€ y están rebajados un 20%. ¿Cuánto le han costado a Jorge los pantalones al pagar en la caja?

1)1ª Forma:

Cf= 75-75*20/100=60€

2) 2ª Forma

HALLAR LA CANTIDAD INICIAL

Otro tipo de problema aparece cuando nos enfrentamos a los porcentajes sabiendo cuál ha sido la subida o la bajada y la cantidad final, pero no conocemos la cantidad inicial.

Para los casos que nos quedan no separaremos entre subida y bajada, ya que se hará de forma similar al caso anterior.

Formas de resolverlo:

1) Cuando conocemos Cf, y el tanto por ciento de subida (o bajada) que vamos a denotar como r, y queremos hallar Co, que la llamaremos x, podemos ir a la ecuación del primer caso y despejar nuestra incógnita: Cf=x±x*r/100= x(1±r/100)→ x= Cf/(1±r/100)

2) Mediante la regla de 3, poniendo en este caso la incógnita en la cantidad inicial:

Ejemplo: En una clase de 4º E.S.O han aprobado un examen de matemáticas 16 alumnos, si estos corresponden al 80% de la clase. ¿Cuántos alumnos hay en la clase?

1) 1ª forma: Si queremos utilizar la fórmula del primer caso, tenemos que tener en cuenta que si han aprobado el 80% supone que han suspendido el 20%, que son los que tendríamos que restar en la fórmula:

16=x-x*20/100= x(1-20/100)→ x= 16/(1-20/100)= 20 alumnos

2) 2ª Forma

HALLAR EL PORCENTAJE QUE SE APLICA

En último lugar, solo nos queda el caso en el que conocida tanto la cantidad inicial y la final, queremos hallar el porcentaje que se ha aplicado.

-Formas de resolverlo:

1) Sabiendo que la cantidad inicial es Co, y la cantidad final es Cf, llamaremos x al porcentaje que se aplica y despejaremos de la ecuación: Cf=Co ±Co*x/100→x=±(Cf-Co)*100/Co

Observación: Recordad que nos dará el porcentaje que equivale a la subida o a la bajada.

2) Aplicando la regla de 3, en este caso la incógnita será el porcentaje final.

Observación: El resultado obtenido en este caso es el porcentaje que se ha pagado, no el de subida o el de bajada.

Ejemplo: Me he comprado unas zapatillas que costaban 56,50€; como la tienda está de liquidación hay un descuento en todos los artículos y al final me han costado 39,50€. ¿Cuál es el porcentaje de la rebaja?

1) 1ª Forma:

39,5=56,50-x/100→x=-(39,50-56,50)*100/56,50=30,1%

2) 2ª Forma:

Por tanto se ha hecho una rebaja de 100-69,9=30,1%.