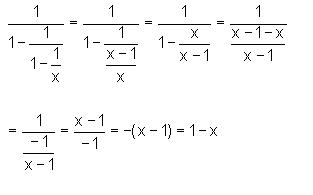Ejercicios de Fracciones algebraicas
Podemos decir que una fracción algebraica es el cociente de dos polinomios, o sea es una expresión de la forma:
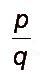
En esta formal p y q son polinomios. p sería el numerador de la fracción, mientras q sería el denominador. Realizar fracciones algebraicas es muy similar a la realización de fracciones aritméticas comunes. En las fracciones algebraicas se destaca la pauta de que el valor de una fracción no se altera en caso de que se multipliquen o se dividan el numerador y el denominador por una misma cifra. Esta cifra debe ser distinta de cero.
Si queremos simplificar una fracción común, debemos dividir el numerador y el denominador entre el mcd, o sea el máximo común divisor de ambos. Pero en caso de querer simplificar una fracción algebraica o sea transformarla en otra equivalente cuya particularidad sea ser una fracción irreducible, debemos factorizar el numerador y el denominador de la fracción. Veamos un ejemplo:
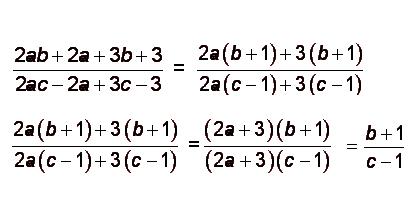
Debemos tener en cuenta que no es correcto simplificar 0/0 o dejar abierta una posibilidad a esto, lo cual sería el producto de no haber establecido las condiciones en una expresión algebraica a simplificarse.
En el siguiente ejemplo veremos los signos asociados a una fracción. Un punto muy importante en esto es saber que si operamos dos de los tres signos no se alterará la fracción:
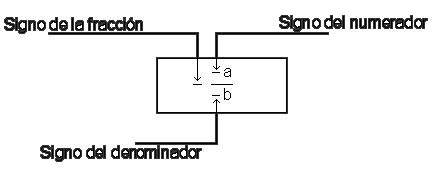
Veamos un claro ejemplo :
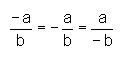
Por último, veremos que es una fracción compuesta. Una fracción compuesta posee una o más fracciones simples en el numerador o en el denominador. Si buscamos reducir fracciones compuestas debemos identificar y reducir luego las fracciones simples por las cuales está compuesta. Veamos un ejemplo: