Identidades logarítmicas
Como ya hemos visto, el logaritmo de un número en una base determinada no es más que el exponente al que debemos elevar la base para poder obtener el número. En el ejemplo siguiente vemos un logaritmo con base b de un número x es el exponente al cual debe elevarse esa misma base para que nos de el número x. Es necesario que la base b sea positiva y distinta de cero. X debe ser un número positivo, y n cualquier número real.
![]()
A la hora de realizar cálculos los logaritmos mantienen determinadas identidades aritméticas que nos serán bastante útiles a la hora de operar con logaritmos. Veremos a continuación cuales son estas identidades.
El logaritmo de un producto de dos números es igual a la suma de los logaritmos de los factores. O sea:
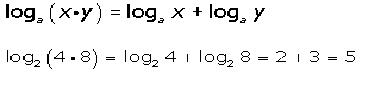
El resultado obtenido se puede generalizar para mas de dos factores, en caso de que Si X1, X2, X3, …, Xn sean n números reales, no nulos y positivos.
El logaritmo de un cociente de dos números es igual al logaritmo del numerador menos el logaritmo del denominador. Entonces:
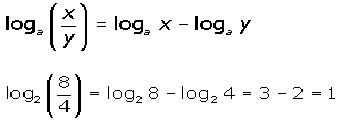
El logaritmo de una potencia es igual al exponente que se multiplica por el logaritmo de la base de la potencia.
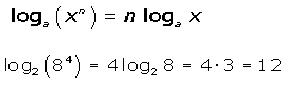
El logaritmo de una raíz es igual al logaritmo del radicando dividido por el índice de la raíz.
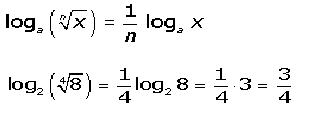
Este caso, es un caso particular de la anterior demostración (logaritmo de una potencia). Las propiedades anteriores se refieren al logaritmo de un producto, cociente, potencia y raíz, pero como podemos ver no hemos dicho nada acerca del logaritmo de una adición o una sustracción, ya que estos no admiten desarrollo.
Hablemos ahora del cambio de base. Los logaritmos que tienen como base el número e, o sea los logaritmos naturales o neperianos, el logaritmo común, el binario o el de base indefinida son frecuentes. Existen entonces infinitos logaritmos dependiendo de la base que se tome. Es posible hacer alteraciones de una base a otra en forma simple. Para esto se utiliza la formula que define el logaritmo de x en base b, si suponemos que b,x y k son números reales positivos y que b y k son distintos de 1.
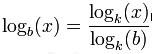
La demostración de esta fórmula sería la siguiente:
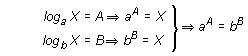
Si tomamos logaritmos en base a en la igualdad anterior, obtenemos:
loga aA = loga bB Þ A loga a = B loga b
Si despejamos b, y tenemos en cuenta que loga=1, se tiene lo siguiente:
![]()
El logaritmo en base imaginaria es un logaritmo que tiene como base la unidad imaginaria. El numero i o unidad imaginaria se define como i=(0,1). Aunque parezca difícil, podemos resolver logaritmos en base imaginaria si aplicamos la siguiente fórmula:
![]()
Z es un número complejo a excepción de cero. Un número complejo describe la suma de un número real y un número imaginario.
