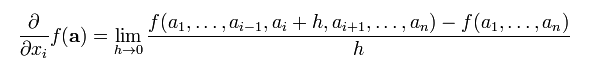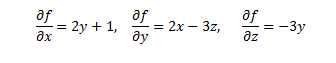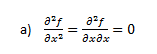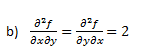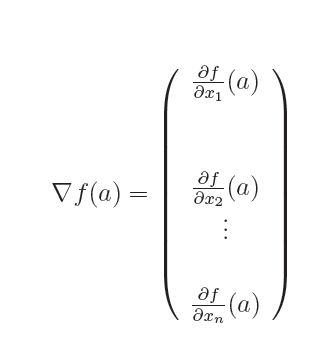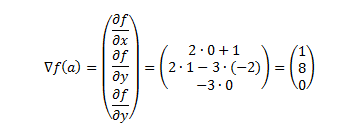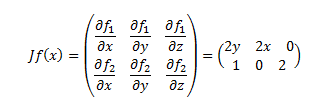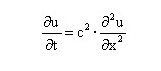Derivadas parciales

Una vez que ya hemos introducido el término de función derivada, podemos estudiar las derivadas parciales. Las derivadas parciales se usan cuando la función que queremos derivar está definida en varias variables, como por ejemplo: f(x,y,z)= 2xy+x-3yz .

DEFINICIÓN

De forma análoga a la definición de derivada en una variable, se define la derivada de una función en varias variables en el punto a=(a1,a2,…….an) como el siguiente límite:

Por tanto es necesario que para poder derivar, derivemos tanto en función de x, en función de y en función de z, de manera independiente. Es decir, en primer lugar derivaríamos en función de x, dejando las demás fijas, como si fueran constantes.

Las derivadas parciales se escriben de las siguientes formas, siendo la más típica la primera de ellas en la que utilizamos la “d redondeada” también conocida como la “d de Jacobi”. Por ejemplo la derivada de f en función de x sería:

Ejemplo 1: A partir del ejemplo anterior, hallemos las derivadas parciales: f(x,y,z)= 2xy+x-3yz

Al igual que definíamos la derivada segunda, como la derivada de la derivada, también existen las derivadas parciales de orden 2, y de manera sucesiva hasta el orden n-ésimo mientras la función sea derivable.

Ejemplo 2: Siguiendo con la función anterior, calculamos las siguientes derivadas:

En el primer apartado, tenemos que derivar respecto de x dos veces, es decir, utilizando la derivada calculada en el ejemplo1, la volvemos a derivar respecto de x.

En el apartado b, tenemos que utilizar la derivada en función de x, y derivarla en función de la y. O lo que es lo mismo, podríamos utilizar la derivada parcial respecto de y, y derivarla respecto de la x.

VECTOR GRADIENTE

Una vez que ya sabemos calcular las derivadas parciales, surgen algún que otro concepto nuevo como el de vector gradiente.

Definición: Llamamos vector gradiente de una función f en el punto a, a un vector columna con n componentes, es decir, una matriz de orden nx1, donde n depende del número de variables en las que está definida f. Se denota como ∇f(a)

Ejemplo 3: El vector gradiente de la función anterior en el punto a=(1,0-2)

MATRIZ JACOBIANA

Cuando no es sólo el dominio de definición el que dependen de varias variables, sino que nuestra imagen también como es en el caso de la siguiente función: f(x,y,z)=(2xy-2, 2z+x), entonces aparece un nuevo concepto, el de matriz jacobiana.

Definición: Llamamos matriz jacobiana de f en el punto a y la denotamos por Jf(a), a la matriz de orden mxn, donde m es la dimensión de la imagen y n es la dimensión del dominio de definición (en nuestro ejemplo sería 2×3), que se obtiene al hacer la traspuesta del vector gradiente de la función de cada una de sus componentes.

Ejemplo: Hallar la matriz jacobiana de f(x,y,z)=(2xy-2, 2z+x) para un punto cualquiera:

Teniendo en cuenta que f1(x,y,z)=2xy-2 ; f2(x,y,z)=2z+x

APLICACIONES DE LAS DERIVADAS PARCIALES

Como es de esperar se utilizan en varias ocasiones en el campo de las matemáticas, pero además van a tener un uso muy importante en al Economía y como es de esperar en la física.

– La aplicación más importante en matemáticas es resolver problemas de optimización (al igual que las derivadas en una dimensión) en varias variables.

– Mientras que en la Economía, el concepto de derivada parcial hace referencia a la marginalidad. De esta manera a partir de una función de coste podemos obtener la función de coste marginal respecto de una u otra variable. Análogamente también podríamos halla la producción marginal o el análisis marginal.

– En Física se utiliza para expresar la ecuación de difusión del calor.