Derivación de funciones trigonométricas

Se llama derivar una función trigonométrica al proceso de hallar un cambio, una diferencia, en la variable independiente. Este cambio se llama derivada, y se representa con un ´, quedando tal que así:

f´(x)=…

Existen tantas derivadas como funciones trigonométricas, en este apartado mostraremos las más importantes con su resolución:

a) Derivada de la función seno.

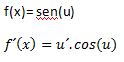
*Nota: La u´ sería la derivada de lo que está dentro del paréntesis.

Ejemplo:

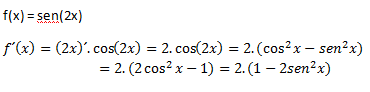
**Pista: Después del primer igual se acaba la derivación, los siguientes pasos surgieron de aplicar las identidades trigonométricas, me ha parecido importante recordarlas, ya que podemos vernos ante problemas en donde haya que transformar las ecuaciones para poder simplificarlas más tarde.

b) Derivada de la función coseno

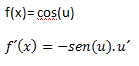
Ejemplo:

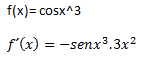
Ya veis que nos siguen haciendo falta las derivadas básicas, así que a darles un repaso, porque sino domináis las básicas no podréis hacer las trigonométricas.

c) Derivada de la función tangente

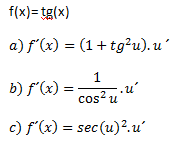
Pues si, la derivada de la tangente tiene estas 3 variantes, no me centraré mucho en ellas, solo decir que tienen su origen en trigonometría, por ejemplo, la secante es la inversa del coseno.

También se podría llegar a la misma conclusión derivando la formula de la tangente:

tg(x)= sen(u)/cos(u)

Pero como hemos dicho, no entraremos en esa parte de la materia. Va a ser mejor para vosotros que os memoricéis estas formulas, pues os aliviaran bastante trabajo y no son muy complejas.

Ejemplo:

 

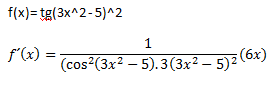
Como veis en este caso aplicamos la opción b.

Conviene no olvidarse nunca

de hacer u´, es decir, lo que está dentro del paréntesis. Procurad realizar varios ejercicios para acostumbrarse a ello.

 

d) Derivada de la función arcoseno

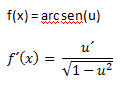
Ejemplo:

 

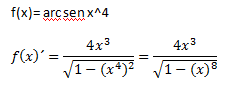
**Nota**: Acordaos de que estamos derivando el arcoseno, no el seno, así que cuando calculamos u´, lo hacemos sobre x^4, os lo comento por si os da la tentación de derivar sen^4. Está separado pero es una sola expresión, arcosen (x).

 

e) Derivada de la función arcocoseno

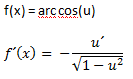
Es exactamente igual que la anterior, pero con un signo menos delante, cuidado de no confundirlas.

 

Hasta aquí las más importantes derivadas de funciones trigonométricas, nos vemos en la siguiente lección.