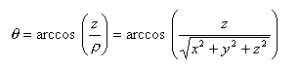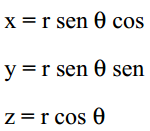Coordenadas esféricas
Ayer vimos que además de las coordenadas cartesianas existen también otro tipo de coordenadas para identificar puntos en el plano, las coordenadas polares que nos sirven para realizar operaciones como integrales de forma más sencilla.
Pues, como ya podéis deducir gracias al título, todavía existen otro tipo de coordenadas para determinar puntos pero en esta ocasión, en el espacio, las coordenadas esféricas. En este sistema de coordenadas para determinar un punto en el espacio necesitamos una distancia, que denominamos radio (r); y dos ángulos, uno de ellos denominado ángulo polar (θ) y el otro azimut ( φ).
COORDENADAS DE UN PUNTO EN COORDENADAS ESFÉRICAS
Como acabamos de mencionar un punto P quedará definido mediante tres cantidades:
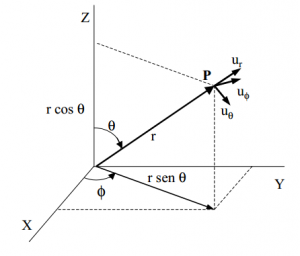
– La distancia o el radio, que denotamos por r (en algunas ocasiones también se denota por la letra griega ρ), y que indica la distancia entre el origen O y el punto P, es decir, el módulo del vector de posición r.
– El ángulo polar, que se denota por la letra griega θ, y que nos indica, tal y como podemos ver en la imagen, el ángulo que forma r con el eje positivo Z.
– El ángulo azimut, que denotamos por φ, que indica el ángulo que forma la proyección de r sobre el eje XY y el eje positivo X.
La base del sistema en el que trabajamos está formada por los vectores ur, uθ y uφ (vectores unitarios, perpendiculares entre sí y linealmente independientes) definidos como:
-La dirección y el sentido del vector ur vienen dadas por la dirección y el sentido que tiene el vector r cuando aumentamos r, manteniendo los ángulos fijos.
-Análogamente, la dirección y el sentido del vector uθ vienen dadas por la dirección y el sentido que tiene r cuando aumentamos θ, manteniendo tanto la distancia por el otro ángulo fijo.
– Por último, la dirección y el sentido del vector uφ quedan determinadas por la dirección y el sentido que tiene el vector r cuando aumentamos φ, manteniendo, en este caso, la distancia y el ángulo θ fijos.
RELACIÓN ENTRE LAS COORDENADAS CARTESIANAS Y ESFÉRICAS
Si nos fijamos en la imagen anterior, podemos deducir como realizar el cambio de coordenadas para pasar de un sistema a otro.
-El radio de la esfera, como ya hemos dicho, es la distancia del punto al origen, por tanto, sería análogo a aplicar el Teorema de Pitágoras, pero con tres dimensiones:
– Por las relaciones trigonométricas del triángulo que se forma, podemos deducir que z= y∙cos θ, luego:
– Utilizando una vez las relaciones trigonométricas, tenemos que la tag φ = y/x, luego:
También podemos deshacer el cambio, para ello tenemos que expresar el valor de x, y, z en función de r, θ y φ, de tal forma que:
Este tipo de coordenadas se utiliza para la resolución de integrales triples, de tal forma que también nos resulte más fácil el método para resolverlas. Pero no es el único sistema de coordenadas que podemos utilizar para determinar puntos en el plano, todavía existe otro más, el sistema de coordenadas cilíndricas, que ya veremos en otro momento.