Continuidad de una función

En una función continua se producen variaciones en los valores de la función para los puntos cercanos del dominio. El dominio es el conjunto de partida de una función, o sea aquellos valores para los cuales la función se define. Entonces la palabra continuidad quiere decir que se produce un pequeño cambio en la variable x o un cambio en el valor f (x). Entonces la gráfica consiste solo de un único trozo de curva ya que no contiene interrupciones. Como definición podemos expresar que una función f (x) es un punto “a” si:

limx->af(x) = f(a).

Es necesario que exista f(a) y debe existir lim x->a f(x) y tiene que ser idéntico a f(a)

Observemos el siguiente ejemplo de trazo continuo propio de una función continua:

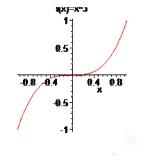
Para que haya continuidad en punto se deben cumplir ciertas condiciones. La primera es que f(a) exista. La función tiene que definirse en el punto en el cual se pretende la continuidad o sea que f(a) ha de ser un número real. En la siguiente condición se cumple que lim f (x) existe. Aquí los valores de la función se aproximan a un solo número real a medida que x se aproxime a “a” por el lado izquierdo por el lado derecho. Como última condición lim f (x)= f (a). Los valores de la función deben acercarse al número real f(a) a medida que x esté próximo a “a” por izquierda y por derecha. Observemos lo siguiente:

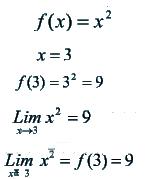
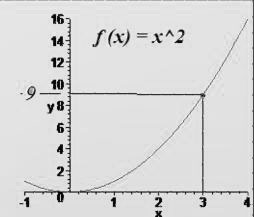
Decimos que una función es continua, cuando tiene continuidad en todo punto de su dominio.

En oposición, cuando una gráfica consta de trozos de curva que se separa por un vacío en una abscisa, se produce una discontinuidad. Veamos ahora un ejemplo de discontinuidad:

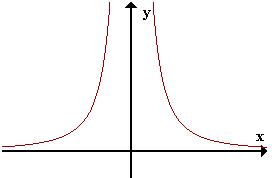
F(x) es igual al cociente de 1 por x al cuadrado. Es discontinua en x=0 ya que no existe f(0)

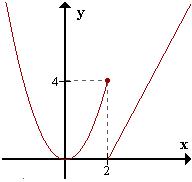
F(x)= x2 si x <= 2 2x - 4 si x > 2

Es discontinua en x=2

Aunque exista f(2) no existe limx->2f(x)

Ya que limx->2-f(x)=4 y limx->2+f(x)=0

Si observamos la función para x próximo a 2 pero menores y dejamos de lado las x mayores que 2, podemos decir que la función es continua en 2 por el lado izquierdo. Una función f(x) es continua por la izquierda si en el punto “a” existe f(a) y lim x->a-f(x) = f(a). En caso que la continuidad sea por la derecha la función f(x) será continua en el punto “a” si existe f(a) y lim x->a+f(x) = f(a). Entonces la función que vimos anteriormente es continua por el lado izquierdo x=2 pero no por el lado derecho.

Las discontinuidades se pueden clasificar de diferentes formas. En el primer caso tenemos las discontinuidades evitables de primera especie en las cuales no existe f(a) pero existe lim x->af(x). Otro caso de discontinuidades evitables sería aquel en el cual existe f(a) y existe lim x->af(x)=b pero b≠f(a). Es decir que existe f(a) pero es diferente al valor del límite. Este último sería una discontinuidad de segunda especie. Tenemos también las discontinuidades no evitables. De primera especie tenemos el caso en que limx->a-f(x) ≠ limx->a+f(x). Decimos aquí entonces que los límites laterales son distintos. En segunda especie no consta el limx->a-f(x) o limx->a+f(x). O sea que en este caso existe uno de los límites laterales.

Una función f(x) es continua en un intervalo cerrado (a,b) si f es continua en a por la derecha o si lo es en b por el lado izquierdo. También si f es continua en x, para todo x que pertenezca al intervalo abierto (a,b).

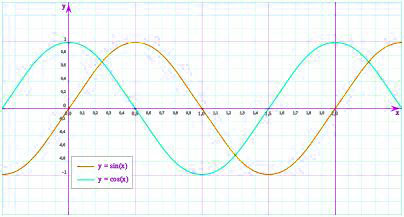
Algunas de las funciones continuas más importantes son las funciones polinomiales, las trigonométricas como el seno y el coseno, las exponenciales y los logaritmos que son continuas en sus referentes dominios de definición. La parábola como función polinómica es un buen ejemplo de continuidad en una función a lo largo de todo el dominio real. En la gráfica siguiente podemos observar la función seno, la cual es periódica y continua en todo el dominio real, ya que tiene carácter periódico. Con el solo hecho de observar uno de sus ciclos comprobamos la continuidad de esta.

Existen algunos teoremas sobre funciones continuas. Nombraremos ahora brevemente cuales son. Uno de ellos es el teorema de Weierstrass que expresa lo siguiente. Si f es continua en [a,b] entonces presentarán los máximos y mínimos absolutos. Otro de los teoremas es el de Bolzano que dice que si f es continua en [a,b] y f(a) > 0 y f(b) < 0, tendremos:

Lo anterior tal que f(c) = 0.

Por último el teorema del valor intermedio en el cual si Si f es continua en [a,b] y f(a) < k < f(b) entonces será:

tal que f(c) = k.

Veamos por último como operar con funciones continuas. Si f y g son funciones continuas en x=a, la suma, producto y división de f y g con g(a) diferente de cero, serán funciones continuas en x=a.

H) f(x) es continua en x=a.

g(x) es continua en x=a.

T) f(x) + g(x) es continua en x=a

Demostremos esto entonces por definición de continuidad.

Existen f(a) y limx->af(x) = f(a)

Existen g(a) y limx->ag(x) = g(a)

Entonces f(x) + g(x) es continua en x=a.

Correlativamente se prueba la continuidad tanto del producto como del cociente.