Completando el cuadrado

Completar el cuadrado es cuando tenemos una ecuación cuadrática como podría ser:

Y la reemplazamos de la siguiente forma:

Primero que nada veremos que pasa si desarrollamos la siguiente ecuación:

Nos quedaría:

Entonces si podemos escribir la ecuación en la forma:

También podemos escribirla seguidamente como:

Esto estaría bastante cerca de lo que queremos demostrar y el trabajo estaría casi hecho. Veamos entonces el caso mas simple que se nos podría presentar. Trabajamos primero con:

Se suma (b/2) al cuadrado y a los dos lados:

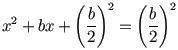
Ahora teniendo en cuenta lo explicado anteriormente, pensemos en que 2d=b entonces d=b/2 Sí, está en la forma :

Aquí tenemos que d=b/2, así que entonces lo escribimos nuevamente y completamos el cuadrado de la siguiente forma:

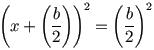
Ahora veamos otro caso que llamaremos caso completo y en cual procederemos como se muestra a continuación:

Probemos ahora con un ejemplo de verdad:

Ahora ya la podemos transformar, y procederemos entonces de la siguiente manera:

En la gráfica que sigue a continuación, el vértice o sea el punto más alto o más bajo de la curva está en (2/3, -19/3) y esos números aparecen en la ecuación.

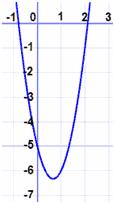
Podemos entonces ahora resolver la ecuación a mano:

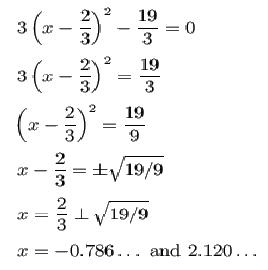
¿Para qué querríamos utilizar la técnica algebraica de completar el cuadrado cuando podríamos utilizar la fórmula cuadrática para resolver las ecuaciones cuadráticas? Lo bueno de esta técnica es que nos facilita el vértice, y también simplifica solucionar la ecuación. Este sería el primer paso en la derivación de la fórmula cuadrática. Muchas veces la forma, puede ser parte de un problema más grande y escribirla como «a(x+d) al cuadrado, mas e» hace más simple llegar al resultado, porque la «x» sólo aparece una sola vez.

Por ejemplo sería difícil integrar la ecuación:

Pero en cambio sería mas facil :

O también «x» puede ser una función (como cos(z)) y de nuevo reescribir puede abrirnos un camino mejor y menos complicado a la solución.