Resta de polinomios
Hola de nuevo, si has llegado hasta aquí, pues, ¡Enhorabuena! ¡Ya eres casi un experto en operaciones polinómicas! Solo nos queda una parte de lección por ver, que se llama resta (o sustracción) de polinomios:
La diferencia de polinomios consiste en restar coeficientes de igual grado (lo que acompaña a las equis, recordemos) entre sí. Este tipo de operaciones, al igual que la suma y la multiplicación poseen una serie de propiedades:
A)Propiedad asociativa: Sean dos polinomios A(x) y B(x) se cumple que:
(A(x) – B(x)) – C(x) = (A(x) – C(x)) – B(x)
B) Elemento Neutro: Sea un polinomio P(x) y 0 un polinomio nulo cuyo valor numérico es cero, se cumple que:
P(x) – 0= P(x)
C) Elemento Opuesto: Siendo A(x) un polinomio y –A(x) su opuesto ( es decir, el mismo polinomio pero cambiado los + por – y los – por + de todos sus coeficientes) se cumple que:
A(x) – A(x) = 0
*Nota: Para aclarar el concepto de elemento opuesto, si no lo entendisteis del todo bien, mirad el ejemplo de abajo, pues el elemento que está restando le hemos cambiado los signos a sus coeficientes, quedándonos el susodicho elemento opuesto.
Pues vamos a ello y hagamos un ejemplo:
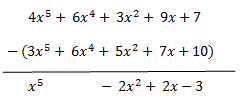
**Pista**: Como observáis, lo único que tenéis que hacer es cambiarle el signo al polinomio que está en el sustraendo, quedando con signo negativo. Dicho esto, solo se tiene que agrupar cada coeficiente de igual grado y proceder a operar. Cabe destacar que bien os puede dar un valor positivo negativo o ningún valor, en este último caso, simplemente lo omitís y dejáis un espacio en blanco (no pongáis cero, no es necesario ya que 0x=0).
Además de estos ejemplos, es importante entender que la resta de polinomios puede ser más compleja cuando se trata de polinomios de grado superior. Por ejemplo, si tienes un polinomio de grado 3 y otro de grado 2, el proceso de resta sigue siendo el mismo, pero debes tener cuidado al alinear los términos de igual grado. Si el polinomio de mayor grado tiene un término que el polinomio de menor grado no tiene, simplemente copias ese término en el resultado.
El siguiente ejercicio tiene los signos alternados, para poner lo más lioso posible, solo os tenéis que fijar antes de operar y acordaros de cambiar cada signo correctamente:
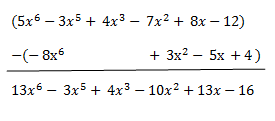
Como se puede apreciar, para realizar correctamente el cálculo, hemos cambiado de signo los coeficientes del sustraendo, quedando todo en la suma del opuesto de ese sustraendo anteriormente citado.
Espero que estos ejemplos te hayan ayudado a entender mejor cómo se realiza la resta de polinomios. Recuerda que la clave está en alinear correctamente los términos de igual grado y cambiar los signos del sustraendo. Con un poco de práctica, te aseguro que te convertirás en un experto en la resta de polinomios.
Y hasta aquí llegamos con las operaciones de polinomios, muchas gracias por vuestra atención y nos leemos en el siguiente artículo 😉
