Polinomios ortogonales
Los polinomios ortogonales son una clase de polinomios que forman una base ortogonal en el espacio de Hilbert (que no es más que una generalización del espacio euclídeo). Aparecen sobretodo en la teoría de ecuaciones diferenciales y en la mecánica cuántica. Veamos la definición exacta de estos polinomios:
Un conjunto de polinomios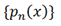 
de orden n, definidos en un determinado intervalo a ≤ x ≤ b, los cuales son ortogonales respecto a una definición de producto interno:
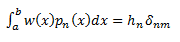
Con w(x)>0 una función de peso en a ≤ x ≤b, que garantiza que la norma sea finita en ese intervalo.
A continuación os dejo un cuadro con las propiedades generales de los polinomios ortogonales, en donde a y b son los límites del intervalo, mientras que Nn indica la norma del polinomio de grado n, siendo w(x) la función de peso, como indicamos anteriormente.
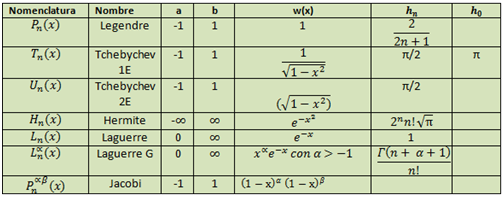
Estos polinomios son conocidos como los «polinomios ortogonales clásicos», y la diferencia con los demás tipos son las siguientes:
A) Para definir los polinomios ortogonales, usamos la fórmula de Rodrigues generalizada:
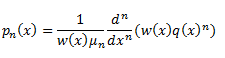
en donde w(x), q y nu vienen detalladas en el cuadro de abajo (y son fijos para cada polinomio ortogonal):
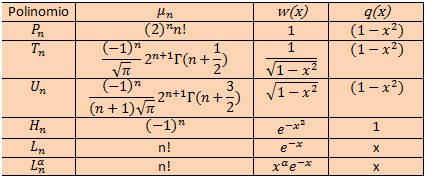
Comentar además que, w(x) es una variable no negativa, e integrable en cierto intervalo de la recta real y p(x) es un polinomio independiente de n, de grado a lo sumo 2.
A continuación os dejo otro cuadro con ejemplos de cómo resolver polinomios ortogonales con la formula antes mencionada.
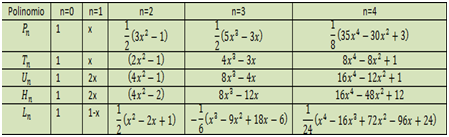
Para resolverlos simplemente tendríamos que sustituir el valor de «n» en la función, considerando el peso y la norma.
B) La última propiedad que diferencia a éstos polinomios de los otros, es que constituyen soluciones de una ecuación diferencial de segundo orden, del tipo:
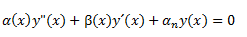
donde alfa y beta son polinomios fijos para cada familia, independientes de n y con grados respectivos dos y uno. El enésimo polinomio es la solución de la ecuación con el correspondiente valor de γn.
Con esto nos despedimos, sígannos visitando en laguia2000 para aprender más cosas sobre el mundo de las matemáticas.