Multiplicación de polinomios

Seguimos con nuestros amigos los polinomios, esta vez, nos toca ver como multiplicar, para ello comenzaremos citando las dos propiedades que se cumplen en la multiplicación de polinomios:

a) Propiedad Asociativa:

– Dados tres polinomios A(x) , B(x) y C(x), se verifica que:

(A(x). B(x)) . C(x)= A(x) . (B(x) . C(x))

b) Propiedad Conmutativa:

-Con dos polinomios A(x) y B(x) se cumple que:

A(x). B(x) = B(x) . A(x)

El orden de los factores no altera el producto, seguramente lo habréis oído alguna vez en clase, pues esto es lo mismo.

c) Existencia del Elemento Neutro, al que llamaremos I(x):

-Siendo A(x) un polinomio de grado n y I(x) un polinomio de grado 1 que tiene como valor la unidad, se cumple que:

A(x) . I(x)= A(x)

Esta propiedad ahora os parecerá de Perogrullo, pero es una muy importante en el álgebra de matrices, que quizás veamos algún día.

Bien, ahora que conocemos las propiedades, pasaremos a explicar cómo se efectúan las multiplicaciones, para ello, dividiremos este tema en tres partes: multiplicación de un número natural por un polinomio, multiplicación de un monomio por un polinomio y

multiplicación de un polinomio por otro polinomio:

 

A) Multiplicación de un número entero por un polinomio:

 

 

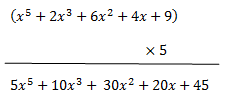
Se trata pues, de multiplicar cada coeficiente de las equis por el número que tenemos debajo, que se llama factor , por cierto (el resultado de una multiplicación de factores, se conoce como producto).

 

B) Multiplicación de un monomio por un polinomio:

 

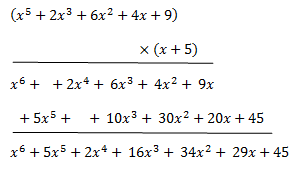
Para multiplicar, he comenzado por el primer término de la izquierda, y a continuación lo he hecho con el termino independiente de la derecha. Tenéis que pensar, cuando hagáis estos ejercicios, en que cada término, bien sea de un polinomio o de un monomio, se resuelve igual que en una multiplicación normal, multiplicando de izquierda a derecha, la única complicación que podéis encontrar, es que con las equis tenéis que multiplicar potencias, pero recordad que cuando se multiplican potencias de igual base, se suman los exponentes, es decir, x^6 multiplicado por x^5 es igual a x^11, ya que 6+5=11.

 

C) Multiplicación de un polinomio por otro polinomio:

Nada más sencillo, pues es lo mismo que hemos hecho en el apartado anterior pero con más componentes, procedemos con otro ejemplo:

 

 

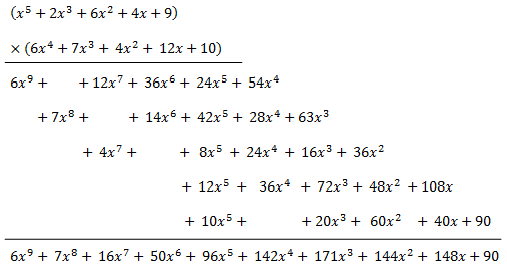
Ha quedado un poco largo el ejemplo, pero no os asustéis, solo tomáoslo con calma y observaréis que no es tanta cosa. Miradlo siempre una segunda vez por si os olvidasteis de poner algo, sobretodo en este caso porque son muchos números y siempre se nos puede pasar alguno.

Hasta aquí llegamos hoy, nos queda muy poco que ver de polinomios, así que animo y paciencia que pronto los dominareis perfectamente, estoy seguro 😉