División de Polinomios

En este apartado os explicaremos una de las operaciones más básicas con polinomios: la división. Ahora bien, seguramente la mayoría de vosotros conoce cómo dividir 25 entre 5 ¿Verdad? Pues la división entre polinomios es exactamente lo mismo, con su divisor, dividendo, cociente y resto.

Antes de empezar es conveniente que sepas algo de producto entre polinomios

Veamos un ejemplo con dos polinomios P(x) y Q(x) :

P(x) = 4x^4 – 2x^3 + 5x^2 + 2x

Q(x)= x^2 – x – 1

 

Quedaría algo como esto :

 

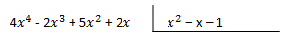
Para realizar la división iremos operando de izquierda a derecha, como si de un cociente normal se tratase, multiplicando el cociente por todos los coeficientes (lo que acompaña a las equis).

 

En el ejemplo podéis observar que multiplico 2x^2 por 2x^2 – x + 1 dando como resultado -4x^4 +2x^3 – 2x^2, después de realizado este cálculo, solo nos queda restar esos dos polinomios, obteniendo un nuevo polinomio más simplificado, con el que deberemos de realizar otra vez las mismas operaciones. ¿Hasta cuándo? Pues hasta que el resto( lo que os sale una vez sumados los polinomios) tenga menor grado que el divisor (en este caso Q(x) ).

Al final nos sale un resto de 23x +15, y ahí lo dejamos, pues es imposible dividirlo entre x^2 -x -1, si no lo tienes muy claro, pregúntate, ¿Por cuál número debería de multiplicar para poder restar 23x? Exacto, no se podría, ya que sus grados son menores ( si estás muy perdido busca el tema de multiplicar polinomios, que subiré en breve).

 

**PISTA** : DIVIDENDO = DIVISOR X COCIENTE + RESTO o lo que es lo mismo, P(x)= Q(x) x C(x) + R(x), si alguna vez tenéis dudas de si va bien alguna división, usad esta fórmula para estar seguros.

En nuestro caso sería: (4x^4 – 2x^3 + 5x^2 + 2x) x ( x^2- x -1) + ( 23x +15) = 4x^4 – 2x^3 + 5x^2 +2x

No pongo detalladas las cuentas por no marearos la cabeza, ya que en otro apartado os explico más a fondo la multiplicación de polinomios.

Seguramente ahora pensareis que es un tostón tener que hacer esto para resolver una simple división, pero…¡No os vayáis! ¡Que hay formas más fáciles! Pues claro, para acercarme más al concepto, os diré que hay distintas formas para factorizar un polinomio en binomios más simples. Seguramente recordareis la Regla de Ruffini que anteriormente hemos tratado, pues bien, esa es una manera de factorizar un polinomio y hallar sus raíces fácilmente para poder operar con ellas.

Hagamos memoria:

P(x) = (x^4 -16) y Q (x)= (x-2), intentábamos dividirlos.

De Ruffini sacábamos esto:

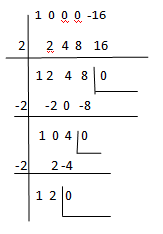
Y nos quedaba una división mucho más sencilla:

 

 

 

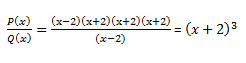
A todo esto mencionaros que Ruffini solo funciona si el divisor (Q(x) en nuestro problema) es un binomio de la forma (ax ± b)ⁿ, en caso contrario no podremos actualizarlo y tendremos que hacerlo » a mano» como aprendimos hoy.