Polinomios
Llamaremos polinomios a las expresiones algebraicas compuestas de dos o más monomios, que son los términos de un polinomio. Podemos definir un polinomio por su grado, clase, y también según el número de términos o monomios. A continuación presentaré algunos ejemplos de estas diferencias para aclarar el tema.
El grado de un polinomio se determina por el término que posee el mayor exponente al que se encuentra la variable x
un polinomio de grado cero podría ser : ![]()
Un polinomio de primer grado : ![]()
Un polinomio de grado dos:![]()
El valor numérico de un polinomio es el resultado de sustituir la variable x por un número cualquiera que sea. Por ejemplo en el siguiente caso :
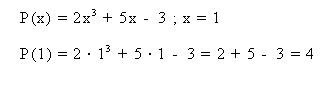
Podemos tener distintas clases de polinomio. El polinomio nulo es aquel que tiene todos sus coeficientes nulos, por ejemplo p(x) =0
El polinomio homogéneo posee todos sus monomios o términos con el mismo grado por ejemplo: ![]()
Un polinomio heterogéneo tiene los términos de diferente grado: 
Un polinomio completo posee todos los términos, por ejemplo en este caso en el cual podemos apreciar desde el término independiente hasta el mayor de primer grado: ![]()
Podemos llamar a un polinomio «ordenado» si los términos que lo conforman están escritos de mayor a menor grado. El siguiente es un buen ejemplo: ![]()
Llamaremos Semejantes a dos polinomios, si se verifica que poseen la misma parte literal: 
Llamaremos iguales a dos polinomios si estos tienen el mismo grado y si lo coeficientes de los monomios de mismo grado son iguales, lo cual podemos apreciar en este ejemplo: 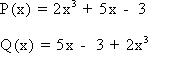
Dos polinomios son opuestos si sus coeficientes de igual grado son opuestos. Para indicar esto se escribe un «-» por delante del polinomio, por ejemplo :
![]()
Podemos clasificar un polinomio según el número de términos que este posea. Un binomio es un polinomio compuesto por dos monomios. Un trinomio es un polinomio compuesto por tres monomios, etc., etc.
Dos polinomios se suman con la adición de los términos de uno y otro, simplificando así, los monomios semejantes que posean el mismo grado. Para realizar la suma de dos polinomios se debe situar uno obre el otro, de manera que coincidan en una misma columna los términos que compartan un mismo grado, de esta forma se procede a la simplificación de términos semejantes. Puede también que se reúnan los términos de igual grado y proceder a sumarlos o restarlos según el signo que posean. El siguiente es un ejemplo de este procedimiento:

En caso de realizar multiplicaciones, se multiplicarán término a término cada monomio de uno por cada monomio de otro, simplificando de esta forma los monomios que sean semejantes. En el siguiente ejemplo veremos la forma de proceder en una multiplicación de polinomios :
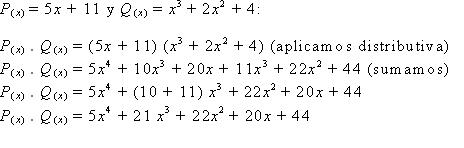
En la división de polinomios existen las mismas partes que en la división aritmética, entonces tenemos dos polinomios, p(x) que sería el dividendo, y q(x) al que llamaremos divisor. El grado de p(x) debe ser mayor que el grado de q(x), el grado de q(x) debe ser mayor o igual a cero. Finalmente siempre tendremos dos polinomios que serían el cociente, C(x) y el resto R(x), lo cual representaremos en el siguiente ejemplo:
![]()
Tal que ![]()
El grado de C(x) se determina por lo que difiere entre los grados p y q, mientras que el grado de R(x) será un grado menor que q. De esta forma para resolver estas operaciones podríamos proceder como se muestra en el siguiente ejemplo:
![]()