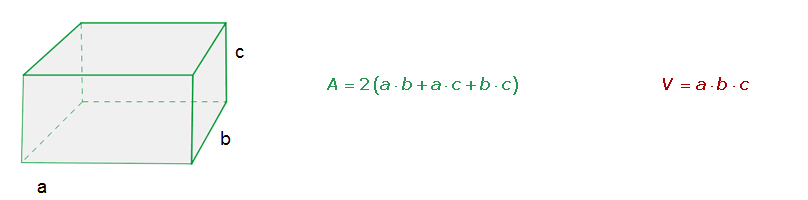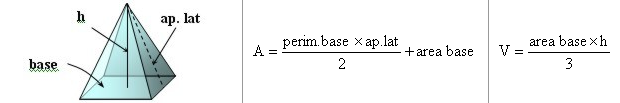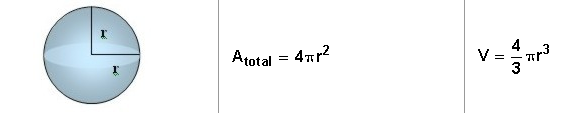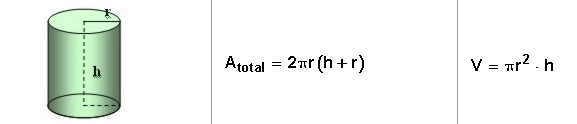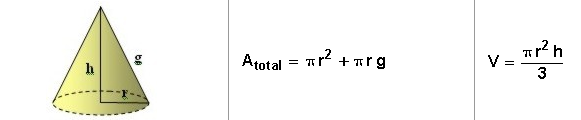Volúmenes de cuerpos geométricos
Hoy vamos estudiar cómo podemos calcular el volumen de los cuerpos geométricos. Para ello comenzaremos recordando la definición de cuerpo geométrico.
Definición: Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, el cual ocupa un volumen en el espacio, es decir, tiene tres dimensiones (ancho, alto y largo) a diferencia de las figuras, las cuales no tienen volumen.
Clasificación: Hay dos tipos de cuerpos geométricos: los poliedros y los no poliedros o cuerpos geométricos redondos.
A continuación veremos los distintos cuerpos geométricos que forman parte de las categorías anteriormente mencionadas, veremos sus elementos y las fórmulas que se utilizan para calcular su superficie ( el área que ocupa el desarrollo plano del cuerpo geométrico) y su volumen.
POLIEDROS
Los poliedros son cuerpos geométricos que están determinados por caras planas encerrando un volumen finito. Los más importantes son los sólidos platónicos: el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro; las pirámides y los prismas. Veamos algunos de ellos detenidamente:
-Cubo: Cada uno de los líneas donde se encuentran dos caras de cualquier cuerpo geométrico se determina arista (a). En el caso del cubo, todas las aristas tienen la misma longitud. Por tanto, para calcular el área, como tiene 6 caras iguales, y el área de cada una es lado por lado (o lado al cuadrado): axa, entonces el área será 6 veces el área de una de sus caras. Por otro lado, el volumen será lado al cubo:
-Ortoedro: Este cuerpo geométrico es un paralelepípedo (al igual que el cubo) en el que todos sus lados son rectángulos. Sea a la base, b el ancho y c la altura, el área y el volumen se calculan de la sigueinte manera:
-Prisma: Un prisma es un cuerpo geométrico que está formado por dos caras iguales y paralelas que reciben el nombre de base y que puede ser cualquier polígono: un cuadrado, un hexágono, un heptágono…; y cuyas caras son paralelogramos. El más común es el caso del prisma rectangular cuyas caras son rectángulos. El área y el volumen se calcularán utilizando las siguientes fórmulas:
– Pirámide: Para poder calcular el área y el volumen de una pirámide en primer lugar es necesario familiarizarnos con sus componentes. Todas las caras de una pirámide son triángulos iguales, por tanto, llamamos apotema o apotema lateral a la altura de los triángulos de sus caras. La altura (h) de una pirámide es la distancia del vértice donde se juntan todas las caras hasta la base. La base de una pirámide puede ser cualquier polígono, al igual que en el caso del prisma.
Por tanto, su área y su volumen vienen dados por:
CUERPOS GEOMÉTRICOS REDONDOS
Los cuerpos redondos, como su nombre indica, son los cuerpos geométricos que tienen una parte redondeada. Dicho con otras palabras, son aquellos que tienen como mínimo una de sus caras con forma curva. Los más conocidos son:
-Esfera: Este cuerpo geométrico se puede decir que no tiene caras, el ejemplo más conocido es de cualquier balón con el que juegan los niños. La distancia desde el centro de la esfera hasta cualquier punto de la superficie se denomina radio (r). Su área y su volumen quedan determinados de la siguiente manera:
-Cilindro: Se podría considerar que el cilindro es el cuerpo geométrico redondo análogo al prisma. Está formado por dos círculos situados paralelamente que se denominan base. Su área y volumen se calculan de la siguiente manera:
-Cono: Por último, el cono. Si hemos dicho que el cilindro es el análogo del prisma; el cono lo sería de la pirámide. A la recta que une un punto del a base con el vértice se le denomina generatriz (g).Su área y su volumen son: