Unión de conjuntos
La teoría de conjuntos es una de las partes de la matemática que se ha desarrollado desde fines del siglo XIX. Ha introducido términos como pertenencia, inclusión, unión y otro. Su uso ha permitido indudablemente mejorar la precisión del lenguaje en áreas de conocimiento como la teoría de relaciones y funciones, la teoría de las probabilidades, entre otras.
Un conjunto es cualquier agrupación o colección de objetos o entidades.
Un elemento es cada uno de los objetos que constituyen un conjunto.
Los conjuntos se designan o escriben generalmente con una letra mayúscula. Sus elementos se encierran entre llaves y si se trata de literales, se usan letras en minúscula. Por ejemplo, el conjunto A, que se forma por los elementos 1, 2 y 3, se escribirá de esta forma:
A= {123}
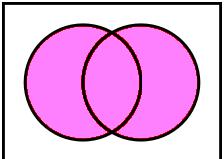
La unión de conjuntos es correspondiente la unificación de los elementos de dos conjunbtos o incluso más conjuntos, que pueden partiendo de esto conformar una nueva forma de conjunto, en la cual los elementos dentro de este correspondan a los elementos de los conjuntos originales. Cuando un elemento es repetido, forma parte del conjunto unión una vez sólamente; esto difiere de la unión de conjuntos en la concepción tradicional de la suma, en la cual los elementos comunes se consideran tantas veces como se encuentren en la totalidad de los conjuntos.
Podemos decir que la unión de conjuntos es una operación binaria (aquella operación matemática, que precisa del operador y de dos argumentos para que se pueda calcular un valor) en el conjunto de todos los subconjuntos de un U, Conjunto universal (Se denomina así al conjunto formado por todos los elementos del tema de referencia) dado. Mediante la cual a cada par de conjuntos A y B de U le es asociado otro conjunto (A U B) de U. Si A y B son dos conjuntos, la unión se define de la siguiente forma :
![]()
AUB
La unión de A y B, es el conjunto de elementos x de U, tal que, x pertenezca a A, o que, x a pertenezca a B.
Esta operación tiene propiedad conmutativa, asociativa y tiene Elemento neutro.
Propiedades
Sean A, B y C tres conjuntos cualesquiera
• A ∪ A = A (propiedad idempotente) En álgebra de conjuntos, las operaciones de unión y también de intersección de conjuntos cumplen con esta propiedad. Esto quiere decir que la unión o intersección de un conjunto con el mismo, resultará en el mismo conjunto.
• A ∪ B = B ∪ A (propiedad conmutativa). Si se cambia el orden de los conjuntos, el conjunto unión no se altera.
• (A ∪ B) ∪ C = A ∪ (B ∪ C) (propiedad asociativa).
• (B ∩ C) ∪ A = (B ∪ A) ∩ (C ∪ A) (propiedad distributiva respecto de la intersección).
• A ∪ (A ∩ B) = A = A ∩ (A ∪ B) (ley de absorción).
Caso particular:
Si un conjunto está incluido en otro, la unión de ambos es el conjunto incluyente.
![]()
Gráficamente:
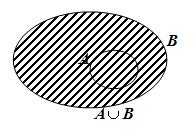
Por lo tanto:
![]()
