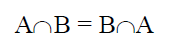Teoría de conjuntos

El principal matemático que es considerado el predecesor de la teoría de conjuntos es George Cantor, un matemático alemán que vivió entre los años 1845 y 1918. La teoría de conjuntos es una rama de las matemáticas que como su nombre indica estudia las propiedades de los conjuntos.

Un conjunto, según palabras de Cantor, es una colección de objetos que están claramente determinados y diferenciados tanto al contemplarlos como en nuestro pensamiento, esta colección de objetos constituyen una totalidad. Cada uno de estos objetos recibe el nombre de elemento.

Para denotar a los conjuntos utilizaremos letras mayúsculas, mientras que para denotar a los elementos utilizaremos letras minúsculas.

Definimos el conjunto vacío, Ø, como un conjunto que no posee ningún elemento.

Diremos A es un subconjunto de B o que un conjunto está contenido en otro, AcB, cuando todos los elementos de A pertenecen a B. Todo conjunto A, tiene dos subconjuntos propios, él mismo y el vacío.

OPERACIONES ENTRE CONJUNTOS

Una vez que ya hemos introducido los conceptos previos de la teoría de conjuntos, vamos a estudiar las operaciones existentes entre los conjuntos y que dan lugar al álgebra de conjuntos.

Intersección

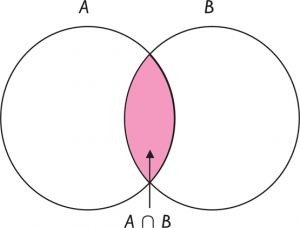La intersección de dos conjuntos, que denotamos por una U invertida, está formada por los elementos que tanto en el conjunto A como en el conjunto B. Es decir, diremos que un elemento pertenece a la intersección de A y B si y sólo si se cumple que xEA y xEB.

Esta operación cumple las siguientes propiedades:

1. Es idempotente, es decir, la intersección de un conjunto consigo mismo da el mismo conjunto.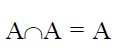

2. Es conmutativa.

3. Es asociativa.

4. Tiene elemento neutro que es el conjunto total, que denotamos por U.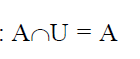

5. Posee elemento absorbente, el conjunto vacío.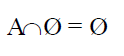

Unión

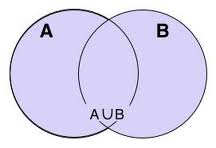La unión de dos conjuntos, que denotamos por U, está formada pos los elementos que pertenecen a A o los elementos que pertenecen a B, así como los que pertenecen a ambos.

La unión verifica las siguientes propiedades:

1. Es idempotente: A U A = A.

2. Es conmutativa: A U B = B U A

3. Es asociativa: (A U B) U C = A U (B U C)

4. Tiene elemento neutro, el vacío:

5. Tiene elemento absorbente, el conjunto total, que denotamos por U: U U A = A

Complementación

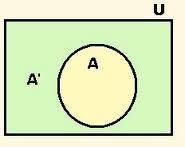El complementario de un conjunto A, se puede denotar de varias formas, por ejemplo como A´ o con un superíndice c; está formado por todos los elementos del espacio total U, que no están en A. Cumple las siguientes propiedades:

1. La unión de un conjunto y su complementario es el espacio total: A U A´=U.

2. La intersección de un conjunto y su complementario es el vacío.

3. El complementario del complementario es el conjunto inicial: (A´)´=A

4. Si AcB, entonces B´cA´.

5. Leyes de Morgan:

Diferencia

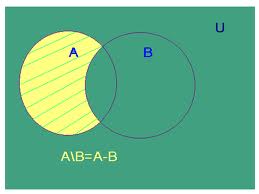La diferencia del conjunto A y B, que denotamos por A-B o AB, está formada por todos los elementos de A que no están en B. Se verifican las siguientes propiedades:

1. Tiene elemento neutro, el vacío: A- Ø=A

2. La diferencia de un conjunto menos él mismo es el vacío: A-A= Ø

Diferencia simétrica

La diferencia simétrica son los elementos que están en A o en B, pero no en ambos. Se puede definir también como la unión de la diferencia de A-B con B-A.

Producto cartesiano

Se llama producto cartesiano de dos conjuntos, y lo denotamos por AxB, al que está formado por los pares (a,b).