Transformaciones trigonométricas

Con las transformaciones trigonométricas podemos convertir una suma o diferencia de seno o cosenos en un doble producto de senos o cosenos, alterando los senos y cosenos de la sustracción o adición de estos.

Es por ello que podemos distinguir varios tipos de transformaciones:

A) De suma (o diferencia) a producto:

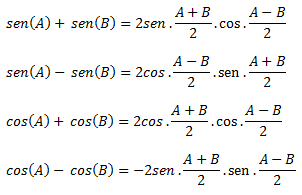
Lo que son las formulas, hay que aprendérselas de memoria. Si bien es más sencillo usar reglar nemotécnicas, por ejemplo, las de los senos, si os fijáis, son exactamente iguales pero cambiando todos los signos y los senos por cosenos (ponerlo todo del revés digamos).

En el caso de los cosenos solo cambian todos los cosenos por senos, no olvidándose nunca ( y esto es importante, porque sino el problema os saldrá mal) del signo menos del 2 en cos(A) –cos(B).

B)De producto a suma o diferencia:

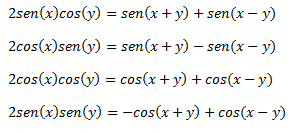
C) De diferencia de cuadrados a producto:

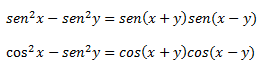
Estos dos últimos tipos de transformaciones tienen también sus truquillos, por ejemplo, en el caso de B), solo se usan senos en los dos primeros productos y cosenos en los dos siguientes. Lo mismo pasa con C), primero senos y después cosenos.

D) Otras transformaciones:

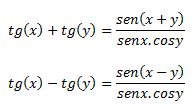
Estás dos no hace falta memorizarlas, pues se pueden deducir con las formulas de senos y cosenos, ya que tgx= senx/cosx, por tanto sustituyendo podemos llegar a la misma conclusión.

Aunque no tienen mucha complicación, pues solo se modifica el numerador, cambiando el signo más por menos.

 

Ejemplos:

 

>>Transformar en producto y calcular:

sen75º – sen15º

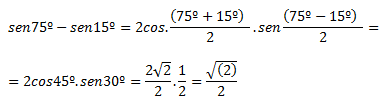
>> Transformar en una suma el siguiente producto:

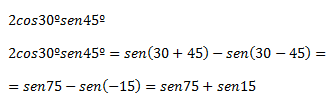
*Nota aquí aplicamos la propiedad de que sen(-x)=-sen(x)

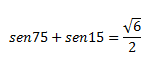
Hemos expresado el resultado en radianes, por motivos de comodidad visual.