Razones trigonométricas
La trigonometría es la rama de matemática que se encarga de estudiar las relaciones entre los lados de los triángulos así como la relación de sus ángulos. Para los cálculos en trigonometría usualmente se emplean las llamadas razones trigonométricas.
Una razón trigonométrica es una razón, o podemos decir también una relación de las longitudes de dos lados de un triángulo rectángulo. Las tres razones trigonométricas habitualmente mas usadas son el seno, el coseno y la tangente. En general aparecen abreviadas como sen cos y tan. Observemos el siguiente recuadro, este nos ayudará a entender claramente a que corresponden estas razones trigonométricas.
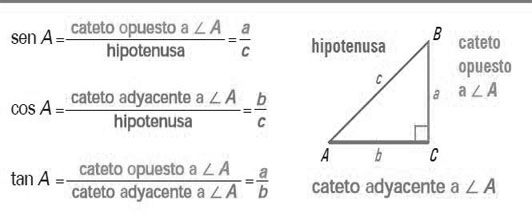
Debemos tener en claro que el valor de una razón trigonométrica no depende del tamaño del triángulo.
Además de las razones trigonométricas básicas, existen otras que son derivadas de estas y que también son de gran utilidad en el estudio de la trigonometría. Estas razones son las recíprocas del seno, coseno y tangente, y se conocen como la secante, la cosecante y la cotangente. Aunque no son tan comúnmente utilizadas como las razones básicas, son fundamentales para entender conceptos más avanzados en trigonometría y en otras ramas de las matemáticas.
La cosecante es la razón recíproca del seno, o también su opuesto multiplicativo. Se abrevia como csc o cosec. Observemos entonces la siguiente fórmula.
![]()
La secante es la razón recíproca del coseno o también su opuesto multiplicativo. Se abrevia como sec.
![]()
La cotangente es la razón recíproca de la tangente o su opuesto multiplicativo. Se abrevia como cot o cta.
![]()
Es importante mencionar que estas razones recíprocas tienen sus propias identidades y propiedades que las relacionan con las razones trigonométricas básicas. Por ejemplo, la identidad fundamental de la trigonometría establece que el cuadrado del seno de un ángulo más el cuadrado del coseno de ese mismo ángulo es igual a uno. De la misma manera, existen identidades que relacionan la secante, la cosecante y la cotangente con el seno, el coseno y la tangente.
Teniendo claro lo anterior veremos ahora un sencillo ejemplo de como hallar las razones trigonométricas. Observemos el siguiente triángulo. Hallaremos el seno, el coseno y la tangente de P y Q.
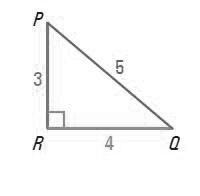
La solución es la siguiente:
La hipotenusa tiene como longitud 5. Para P, la longitud del cateto opuesto es 4 y la longitud del cateto adyacente es 3. Observemos entonces lo siguiente:

Para Q, la longitud del cateto opuesto nos da como resultado 3, y la longitud del cateto adyacente 4.

Además de calcular las razones trigonométricas básicas, también podemos calcular las razones recíprocas. Para ello, simplemente tomamos el recíproco de los valores obtenidos para el seno, el coseno y la tangente. Por ejemplo, la secante de P será el recíproco del coseno de P, es decir, 5/3. De la misma manera, podemos calcular la cosecante y la cotangente de P y Q.
