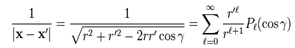Polinomios de Laguerre

Para estos polinomios se utiliza una fórmula idéntica la usada para los polinomios anteriormente explicados:

Considerando el espacio de dos funciones reales de cuadro integrables con respecto al peso w(x)>0, en el intervalo (0,∞):

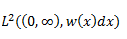
Es decir:

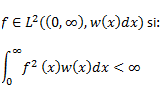
Aplicando el producto interno al espacio descrito:

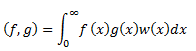
Para encontrar nuestro polinomio, necesitamos que sea ortogonal respecto a su producto interno. Esto lo podemos hacer gracias a la Fórmula de Rodrigues (explicada en apartados anteriores).

Voy a poner tan solo el paso final de esa fórmula, pues nos va a venir bien para explicar de dónde sale w(x) (el peso):

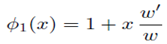
Estamos por tanto, despejando de la Formula de Rodrigues cuando n=1.

Si suponemos que q1(x)=A+Bx, se obtiene la siguiente ecuación diferencial:

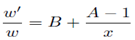
Y después de integrar, nos sale:

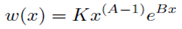
Siendo K una constante cualquiera positiva. Si exigimos que K=1 y que, por tanto, B<0:

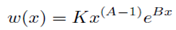
Tendremos nuestra función de peso.

Ahora ya podemos crear nuestra ecuación generalizada para los polinomios de Laguerre:

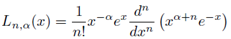
A continuación adjunto una tabla con los primeros polinomios de Laguerre, que se pueden sacar mediante esta expresión (siempre considerando α>-1):

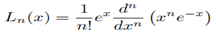
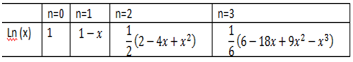
Para no variar vamos a poner las propiedades de los polinomios de Laguerre:

a) Función generatriz:

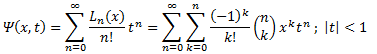
b) Ortogonalidad:

Los polinomios de Laguerre son ortogonales, según el producto escalar:

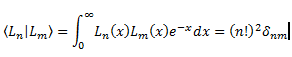
Sin embargo, estas funciones se pueden definir como:

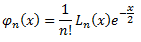
Y además, son ortonormales con respecto del producto escalar ordinario:

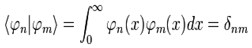
c) Los polinomios de Laguerre son simétricos o antisimetricos, tal que:

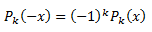
En cuanto a las aplicaciones de estos polinomios, se destacan en la Física y en el cálculo numérico, ya que, gracias a éste último permiten el cómputo de integrales definidas sin necesidad de usar fórmulas analíticas, tan sólo fijando como intervalo de integración los limites [-1;1].

También es importante su aportación al desarrollo por serie, de ecuaciones como: