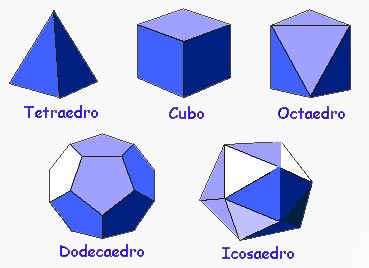
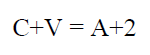Sólidos platónicos

Los sólidos platónicos son cuerpos geométricos que se caracterizan por:

– ser poliedros convexos

– todas sus caras están formadas por polígonos regulares (polígonos con todos los lados y ángulos iguales) iguales

– en cada uno de sus vértices, se unen el mismo número de caras.

Sólo existen cinco sólidos platónicos: el tetraedro, el cubo ( el dado de toda la vida), el octaedro, el dodecaedro y el icosaedro, cuyas características estudiaremos a continuación.

El estudio de los sólidos platónicos se remonta muchos siglos atrás, siendo estudiados por primera vez en la antigua Grecia, alrededor del año 530 a.C. en la escuela pitagórica, fundada como su nombre indica por Pitágoras, (de hecho en un principio se llamaron sólidos pitagóricos). Pero tras ser citados en la obra de Platón “El Timeo”, pasaron a llamarse sólidos platónicos. En esta obra es donde se resalta el carácter trascendental de estos poliedros, donde se asocia a cada uno de ellos un elemento, de tal forma que:

– El tetraedo simboliza el fuego

– El cubo simboliza la tierra

– El octaedro simboliza el aire

– El icosaedro el agua

– Y el dodecaedro, el quinto elemento que simboliza el todo, el cosmos.

Una vez hecha la introducción histórica, pasamos al estudio de cada uno de los sólidos platónicos:

– El tetraedro está formado por 4 triángulos equiláteros.

– El cubo, también conocido con el nombre de hexaedro regular, está formado por 6 cuadrados.

– El octaedro lo forman 8 triángulos equiláteros.

– El dodecaedro está formado por 12 pentágonos regulares

– Y por último, el icosaedro está formado por 20 triángulos equiláteros.

CARACTERÍSTICAS DE LOS SÓLIDOS PLATÓNICOS

Además de las características fundamentes necesarias mencionadas al comienzo, estas figuras geométricas cumplen otras muchas debido a su construcción.

Son simétricos, es más, cumplen todas las simetrías conocidas:

– Son simétricos respecto a un punto, denominado punto central, que es el centro de simetría.

– Son simétricos respecto a un eje, a decir verdad, tienen varios ejes de simetría cuya característica común es que pasan por el centro de simetría.

– Son simétrico respecto a un plano, al igual que en el caso anterior, encontramos simetría respecto a varios planos caracterizados por contener al centro de simetría, así como combinaciones de los ejes de simetría.

Son duales. Decimos que un poliedro es dual a otro que se obtiene al coger los centros de las caras del primer poliedro y convertirlos en vértices del nuevo. Se establece de esta forma una reciprocidad entre el número de caras y el de vértices de un poliedro y su dual. Se tiene por tanto que:

– El cubo y el octaedro son duales entre sí

– El icosaedro y el dodecaedro también son duales entre sí.

Cumplen el teorema de Euler:

Donde C es el número de caras, V es el número de vértices y A es el número de aristas. Este teorema se utiliza para demostrar que sólo existen cinco sólidos platónicos y que son únicamente los que hemos mencionado.