Suma de fracciones
En matemática decimos que una fracción es la expresión de una cantidad la cual es dividida entre otra. Pueden representarse de diversas formas. Las fracciones son números racionales ya que el numerador y el denominador son números enteros. El denominador es el número inferior en una fracción, representa la cantidad de porciones en las cuales se ha dividido la unidad y también le da el nombre y clasifica a la fracción, puede ser en medios, tercios, cuartos, etc. Podemos decir también que el numerador es el dividendo mientras el denominador es el divisor.
Además de la suma, las fracciones también pueden ser restadas, multiplicadas y divididas. Cada una de estas operaciones tiene sus propias reglas y procedimientos, pero todas ellas requieren un buen entendimiento de los conceptos fundamentales de las fracciones.
Para sumar fracciones debemos tener en cuenta que se nos pueden presentar dos casos diferentes. Uno de ellos con fracciones que tienen el mismo denominador. En este caso si sumamos dos o más fracciones en las cuales se cuenta con el mismo denominador, la forma de sumar será bastante sencilla. Tan sólo debemos sumar los numeradores y debemos dejar el denominador común. Por ejemplo:
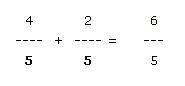
En el segundo caso, se suman fracciones de distinto denominador. Este caso no es tan sencillo como el anterior, y debemos seguir algunos pasos indispensables para poder realizarlo. En primer lugar debemos reducir las dos fracciones al mínimo común múltiplo de los denominadores. Luego de esto calcularemos el numerador con la siguiente fórmula. Numerador antiguo multiplicado por denominador común y dividido luego por denominador antiguo. En último lugar procederemos como en el primer caso, ya que si realizamos los pasos anteriores, las fracciones tendrán el mismo denominador. Veamos un ejemplo:

Primero calcularemos entonces el m.c.m (mínimo común múltiplo)
m.c.m (4,2)=4
Luego calculamos los numeradores:
El numerador de la primera fracción es 3×4 :4=3
El numerador de la segunda fracción es: 4×4:2=8
Nos quedará entonces una suma con las siguientes fracciones:

Podemos observar entonces que los denominadores son exactos, siendo así podemos proceder a la suma como en el primer caso explicado. Veamos como no quedaría:
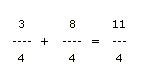
Es importante recordar que las fracciones son una forma de representar una división. En otras palabras, una fracción es una forma de representar un número que no es un número entero. Esto significa que las fracciones pueden ser utilizadas para representar cantidades que son más pequeñas que un número entero, o para representar cantidades que son más grandes que un número entero pero que no son números enteros exactos.
Además, las fracciones también pueden ser utilizadas para representar relaciones entre dos cantidades. Por ejemplo, si tienes dos manzanas y tres naranjas, puedes representar esta relación como una fracción: 2/3. Esto significa que por cada dos manzanas, tienes tres naranjas.
En resumen, las fracciones son una herramienta matemática extremadamente útil que nos permite representar y trabajar con cantidades que no son números enteros. Ya sea que estés sumando fracciones, restando fracciones, multiplicando fracciones o dividiendo fracciones, es importante entender cómo funcionan las fracciones y cómo se pueden utilizar para resolver problemas matemáticos.
