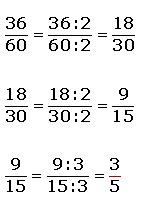Simplificación de fracciones
Una fracción es un número que se escribe de forma a/b, b nunca puede ser cero. Este tipo de números son números racionales. El numerador es el número que se encuentra arriba en la fracción o quebrado mientras el número que se encuentra abajo es el denominador.
Simplificar una fracción es transformarla en una fracción equivalente más simple. La fracción a simplificar se debe seguir simplificando hasta llegar entonces a una fracción que ya no se pueda simplificar más, a esta le damos el nombre de fracción irreducible. Para realizar una simplificación de fracciones lo que debemos hacer es dividir el numerador y el denominador, ambos por un mismo número. Por lo tanto debe haber un número entre el cual podamos dividir el numerador y el denominador de forma exacta, o sea que lo correcto para realizar la simplificación sería buscar algún divisor en común (debemos tener en cuenta que no pueden ser primos entre si). Lo mejor es seguir un orden metódico, o sea intentar dividir por ejemplo entre 2, luego probar con el 3, y así continuamente. Podriamos para hacer esto utilizar los números primos.Veamos algunos ejemplos:
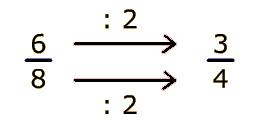
En el siguiente ejemplo observamos que no es posible realizar una simplificación, ya que el numerador y el denominador, son números primos entre si.
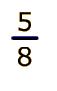
En caso de que tanto el denominador como el numerador terminen en cero, podemos hacer una simplificación rápida y eficaz, veamos un ejemplo:
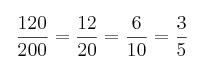
Es mucho mejor y efectivo, para realizar simplificaciones de fracciones, tener en cuenta las reglas de divisibilidad. Las mas usadas son las reglas de divsibilidad de 2, 3, y 5.
Si un número termina en 0, 2, 4, 6, 8, el número es divisible entre dos, como lo serían las cifras, 26, 14, 38, etc. Etc.
Si la suma de los dígitos de un número nos da como resultado un múltiplo de tres, significa que la cifra es divisible entre 3. Por ejemplo 102. 1+0+2 =3 si multiplicamos 3 por 34 nos dará como resultado 102.
Un número es divisible entre 5, si termina en 5 ó 0, por ejemplo, 100, 55, 50, 25.
Otras reglas que podemos usar, y que también nos dará un resultado sin resto o residuo, son las siguientes:
Es divisible entre 4 aquel número en el cual sus dos últimos dígitos forman un número divisible entre 4.
Si el número es par y la suma de sus dígitos da como resultado un número divisible entre 3, será divisible entre 6.
Si la suma de los dígitos da un número divisible entre 9, será entonces la cifra es divisible entre 9.
Por último veamos algunos otros ejemplos para aclarar este tema: