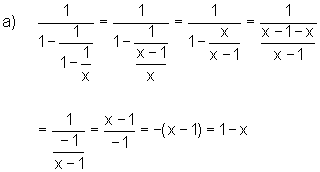Fracciones algebraicas
Las fracciones algebraicas son los cociente de dos expresiones algebraicas. Si una fracción algebraica es el cociente de dos polinomios, la llamaremos fracción racional. Una fracción algebraica es una expresión de la forma:
![]()
El numerador de la facción es a mientras b sería el denominador de la fracción. Debemos tener en cuenta que la mecanización de fracciones algebraicas está relacionada y tiene mucho en común con la mecanización de fracciones comunes en aritmética.
Debemos saber que para simplificar una fracción en aritmética, se divide el numerador y el denominador entre el máximo común divisor de estos. El valor de una fracción no se alterará si se multiplican o dividen, el numerador y el denominador por un mismo número. Este número debe ser siempre distinto de cero. De otra forma podriamos decir que la simplificación de una fracción se obtiene factorizando el numerador y el denominador. Observemos el siguiente ejemplo:
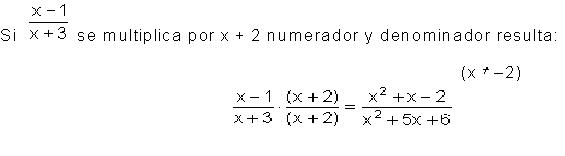
Aprenderemos ahora que quiere decir simplificar una fracción. Reducir una fracción o simplificarla es lo mismo que transformarla a otra fracción equivalente cuya particularidad sea ser irreducible. El siguiente ejemplo es adecuado para esto:

Es muy importante expresar que x no sea igual a – 2 para poder simplificar la fracción. Por lo tanto no es correcto simplificar una fracción 0/0 o dejar posibilidad a esto, lo cual sería producto de no haber determinado las condiciones adecuadas en una expresión algebraica a simplificar.
Debemos ser cuidadosos al simplificar fracciones ya que hay errores muy comunes, debido a la aplicación de fórmulas incorrectas, por ejemplo en los siguientes casos:
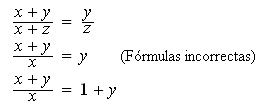
En las sumas y restas algebraicas debemos proceder a simplificar a un común denominador, manteniendo a este y sumando o restando los numeradores , simplificando luego la fracción resultante. Existen dos casos que se nos pueden presentar. El primero es que tengamos un mismo denominador. Observemos el siguiente ejemplo :
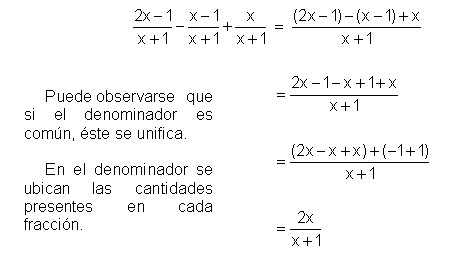
El segundo caso es aquel en el cual tenemos un distinto denominador. Mediante el mínimo común múltiplo (M.C.M) las fracciones con denominadores distintos se convierten en fracciones equivalentes de denominador común. Observemos la siguiente fraccion común, con su solución:
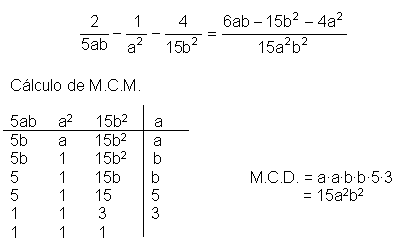
De otra forma Encontrado el M.C.M se multiplicará cada fracción, numeradores y denominadores por los terminos que faltan, observemos lo siguiente:
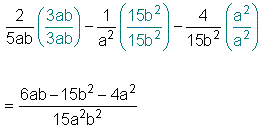
El producto de dos fracciones algebraicas es el producto de sus respectivos numeradores partido por el producto de sus denominadores. Antes de multiplicar debemos simplificar en lo posible. Sea a/b una fracción algebraica cualquiera que sea que esté multiplicada por una c/d diremos entonces que :
![]()
El cociente de dos fracciones algebraicas es el resultado del producto de la primera por la inversa de la segunda, esto es el producto cruzado de términos. Sea entonces a/b una fracción algebraica cualquiera que se divida entre otra c/d, diremos entonces :
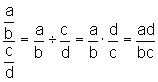
Podemos encontrar fracciones inversas, esto significa que una fracción tiene los mismos terminos de otra pero invertidos. Esto se utiliza en procedimientos tales como la realización de una división.
Como último punto hablaremos de fracciones compuestas. Llamaremos a una fracción “compuesta” cuando esta posea una o más fracciones simples en el numerador y/o denominador. Para simplificar o reducir fracciones compuestas , debemos identificar y reducir las fracciones simples de las que se compone. El siguiente es un claro ejemplo de esto: