Series de Dirichlet
Una serie de Dirichlet es aquella que cumple:
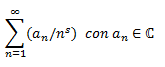
donde s y an son números complejos, con n=1,2,3,4…
Dicho de una forma más clara, para qué sirve esto de las series de Dirichlet, se usan para intentar demostrar que:
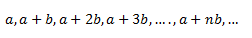
Con a y b números primos relativos (no tienen otro divisor común más que 1 y -1, vamos, que son primos solamente entre sí), se puede encontrar un número infinito de números primos.
Esta hipótesis viene reflejada en la primera formula, pero dicho de una forma más práctica.
Se usan sobretodo en la Teoría Analítica de Números, además de otras áreas fuera de este campo. Quizás la más conocida aportación sea la definición de la zeta de Riemann, la cual es una serie de Dirichlet.
Lo que se busca es saber cuándo una serie converge de forma absoluta, es decir:
1º) Hay un número extendido real L tal que:
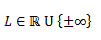
Que cumple la propiedad de las series e Dirichlet, mencionada al principio:
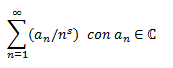
2º) Converge de forma absoluta para Re (s) >L, pero no para Re(s)<L.
Dicho de otro modo, para cualquier ∈>0, la convergencia es uniforme en:
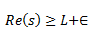
Así que la serie representa una función holomorfa para todo Re(s)>L
Vamos a profundizar un poco más en la relación con la función de Riemann:
De acuerdo a este teorema, si s es una variable compleja tal que:
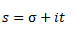
en donde σ y t son números reales.
Entonces:

Con esto se prueba que:
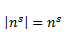
Puesto que:
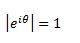
para θ real.
