Función generadora

Cuando hablamos de función generadora o nos estamos refiriendo a una serie de potencias. Los coeficientes de dichas potencias recopilan datos sobre una sucesión an, los índices de esta parten de los números enteros positivos. Veamos ahora el siguiente ejemplo que nos ayudará a comprender rápidamente que es una función generadora.

Vamos a suponer que un terrateniente desea compartir sus doce haciendas entre sus tres hijos, de manera que el mayor tenga como mínimo cuatro haciendas, el mediano tres haciendas y el menor dos haciendas. El padre también quiere que ninguno de sus hijos llegue a tener más de 6 haciendas. Entonces ¿de cuantas formas el terrateniente puede efectuar el reparto?

Nombremos como x1, x2 y x3, el número de haciendas que recibe el hijo mayor, el mediano y el menor, para porceder a solucionar la cuestión. Para esto debemos poder hallar todas las soluciones de la siguiente ecuación,

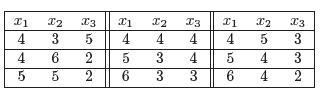
El total de soluciones de este ejercicio se puede observar en la tabla que vemos a continuación,

Vamos a Pensar ahora la forma de multiplicación de los polinomios,

Veamos de cuantos modos podemos obtener x elevado a 12, por ejemplo,

Se puede observar que obtiene x elevado a 12, lo cual es correspondiente a cada una de las ternas de la tabla anterior. Así, la solución del problema es el coeficiente de x elevado a 12.

Esta función es lo que denominamos función generadora del problema, sus coeficientes proporcionan la solución de un conjunto con problemas relacionados. Por ejemplo si se trata de efectuar el reparto de 13 haciendas, con las mismas limitaciones, la solución será correspondiente al coeficiente x elevado a 13 en f(x) o sea que habrían 11 posibles formas de reparto.

El método para este tipo de funciones suministra la idea de plantear un problema de distribución con limitaciones.

Definición:

Llamaremos función generadora o generatriz de una sucesión a0, a1, a2 de reales {an} n≥0 a la función G(x) tal que,

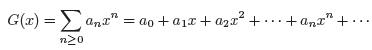
La función generatriz de la sucesión {an} n≥0 se puede describir como una forma diferente de representación. Veamos algunos ejemplos.

A razón del teorema del binomio de Newton se puede escribir lo siguiente,

De este modo Podemos decir que,

La siguiente función

se encarga de resumir la solucion de problemas, comopor ejemplo determinar el número de formas en que pueden ser seleccionados k objetos de un total de n.

Otro ejemplo de funciones generadoras lo podemos hallar en los números de Stirling de primera clase.

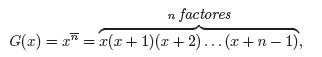
Genera la sucesión,

De este modo una permutación de n elementos se puede descomponer en k ciclos.

Propiedades más importantes

• Adición.

Si G1(x) corresponde a una función generatriz de a0,a1,….y G2(x) es la función generatriz de b0,b1… tenemos que,

Solo en necesario tener en claro que las series se suman tal como los polinomios.

• Desplazamiento.

Si G(x) es la función generatriz de a0, a1,….., entonces,

es la función generatriz de,

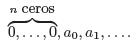
Correlativamente,

• Producto.

Si G1(x) es la función generatriz de a1, a2,…y G2 lo es de b0,b1…., tenemos que

Sería la función generatriz o generadora de la sucesión s0, s1…., donde,

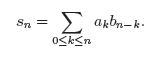
En términos de series de potencias a la serie,

Llamamos producto de Cauchy de las series o términos definidos por una sucesión, definida por G1(x) y G2(x).

Un caso interesante es si {bn} corresponde a la sucesión constante 1. Entonces tenemos que,

La cual es la función generatriz de la sucesión de lo que son sumas de modo parcial de la sucesión {an} n≥0

Hay varios tipos de funciones generadoras, funciones generadoras ordinarias, funciones generadoras exponenciales, la serie de Lambert, la serie de Bell y la serie de Dirichlet.