Racionalización de fracciones

Cuando hablamos de racionalizar, necesariamente nos referiremos a un método para eliminar radicales del denominador de unas determinadas fracciones. Esta eliminación se consigue por medio de fracciones equivalentes a las anteriores.

Es importante entender que la racionalización de fracciones es una técnica fundamental en matemáticas, especialmente en álgebra y cálculo. Esta técnica nos permite simplificar las fracciones y hacerlas más manejables para operaciones posteriores. Además, la racionalización de fracciones es un paso crucial en la resolución de ecuaciones y problemas matemáticos más complejos.

Vamos a ver caso a caso que nos podemos encontrar:

a) Denominador formado por una sola raíz cuadrada.

Este es el caso más sencillo, solamente necesitamos multiplicar el numerador y denominador por una fracción que contenga esa misma raíz. Pongo ejemplo, para que se vea más claro:

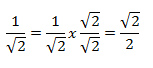
La raíz se elimina, pues, si recordáis, los radicales se pueden poner en forma de potencia, con lo que al multiplicar 1/2 por 1/2 nos quedaría 2/2=1, que es a lo que está elevado el denominador resultante.

b) Uno de los términos del denominador (o en los dos) hay una raíz cuadrada.

Para este caso, puede parecer complicado, pero solo habrá que multiplicar esa expresión por su conjugado, es decir, en caso de tener una resta, multiplicarlo por una suma y viceversa, con esto aplicaremos la regla de suma por diferencia, diferencia de cuadrados y eliminaremos los radicales.

Es importante recordar que el conjugado de un número complejo es el número que se obtiene al cambiar el signo de su parte imaginaria. Por lo tanto, si nuestro número es a + bi, su conjugado será a – bi. Esta propiedad es muy útil en la racionalización de fracciones.

Ejemplo:

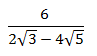
En este ejemplo, primero nos compensa simplificar los coeficientes no radicales, es decir, vamos a reducir ese 6, 2 y 4:

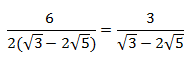
Ahora podemos dedicarnos a racionalizar, multiplicando, tanto numerador, como denominador, por el conjugado de éste último:

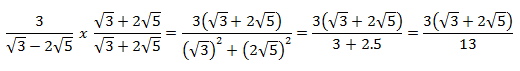
Si en vez de una resta tuviésemos una suma, procederíamos igual, pero multiplicando el cociente por lo mismo que haya en el denominador pero en forma de resta.

c) Raíz mayor que dos en el denominador.

Consideramos que no hay ningún binomio presente, solamente un radical. Lo que tenemos que conseguir es que el número que está dentro del radical(el llamado radicando), esté elevado al mismo índice que la raíz, es decir, si es una raíz cúbica, conseguir un cubo, si es una raíz cuarta, conseguir un elevado a cuatro, y así sucesivamente.

Este proceso puede parecer complicado al principio, pero con práctica se vuelve más fácil. Es importante recordar que la clave para racionalizar una fracción con una raíz cúbica en el denominador es encontrar una fracción equivalente con un denominador que sea un cubo perfecto.

Ejemplo:

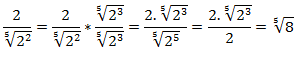
Tenemos que concentrarnos, pues, en el denominador, en ese radical, fijarnos en el índice de la raíz, compararlo con el exponente del radicando, y después, multiplicarlo por un radical con un radicando elevado a la diferencia entre el índice de la raíz y el exponente del radicando.

La racionalización de fracciones es una habilidad esencial en matemáticas. Aunque puede parecer complicado al principio, con práctica y entendimiento de los conceptos básicos, se puede dominar esta técnica. Recuerda, la clave para racionalizar una fracción es encontrar una fracción equivalente con un denominador racional.