Multiplicidad
La multiplicidad se refiere al carácter de múltiple o también a la multitud y abundancia excesiva de los individuos, acontecimientos, etc. La palabra tiene su origen en el término latino multiplicitas.
En las ciencias matemáticas, la multiplicidad de un miembro, segmento o porción de un multiconjunto es correspondiente a la cantidad de pertenencias de este en el multiconjunto. Por ejemplo, esta expresión es utilizada para hacer referencia al número de veces que un polinomio tiene raíz en un punto establecido.
La multiplicidad en factores primos es conocida como factorización, este es un concepto algebraico que describe cuando se descompone un número en el producto de otros más pequeños que si son multiplicados en su totalidad resultará el número original, por ejemplo:
60=2.2.3.5
Además, en el ámbito de la física y la química, la multiplicidad también tiene un significado importante. En la teoría cuántica de campos, la multiplicidad se refiere al número de estados independientes que tienen la misma energía, es decir, el número de formas en que se puede organizar un sistema sin cambiar su energía total. En la química, la multiplicidad de un estado electrónico se define como el número máximo de electrones con la misma energía que puede tener un átomo o una molécula, y se calcula como 2S+1, donde S es el spin total.
Multiplicidad de la raíz de un polinomio
Sea F un campo (estructura algebraica en la cual las operaciones como la suma y la multiplicación pueden ser realizadas y cumplen las propiedades asociativa, conmutativa y distributiva) y p(x) un polinomio de una variable con coeficientes en F. Un elemento a ∈ F se denomina raíz de multiplicidad k de p(x) cuando hay un polinomio s(x) tal que,
![]()
entonces a recibirá el calificativo de raíz simple.
Veamos un ejemplo, el siguiente polinomio:
![]()
tiene como raíces a 1 y − 4 y puede escribirse de esta forma,
![]()
Esto significa que 1 es una raíz de multiplicidad 2, y − 4 es correspondiente a una raíz simple.(multiplicidad 1).
Multiplicidad de cero en una función
Sea I un intervalo de R y F una función de I a R o C y C ∈ I sea un cero de F, por ejemplo, un punto tal que F ( C) = 0. El punto C tomará el nombre de cero de multiplicidad K de F si existe un número real I ≠ 0 tal que,
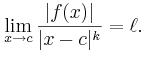
De forma más habitual, siendo F una función de un subconjunto abierto A en este caso de un espacio vectorial (objeto básico de estudio en la rama de las ciencias matemáticas denominada álgebra lineal. Los elementos de los espacios vectoriales son llamados vectores) con norma E en un espacio vectorial con norma F, y sea C ∈ A cero de F, por ejemplo, un punto tal que F(C ) =0. El punto C toma el nombre de cero de multiplicidad K de F si existe un número real I ≠ tal que,
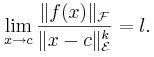
El punto C se denomina cero de multiplicidad ∞ de F si para cada K, se cumple lo siguiente,
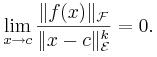
Ejemplo 1. Dado que,
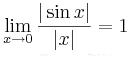
0 es un cero de multiplicidad 1 de la función seno.
Ejemplo 2. Si tenemos que,
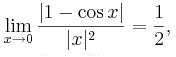
0 es un cero de multiplicidad 2 de la función 1- COS.
Ejemplo 3. Si consideramos la función F de R en R tal que,
![]()
Lo anterior solo si x ≠ 0.
Por lo cual, dado que,
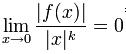
Para todo k ∈ N, 0 es un cero de multiplicidad ∞ para la función F.
La multiplicidad algebraica y geométrica
La multiplicidad algebraica por ejemplo AM de un valor característico A corresponde a la cantidad de veces que surge A como la raíz de det(A- λI)=0. Un valor característico de multiplicidad algebraica 1 es denominado «valor propio simple». Por otro lado la multiplicidad geométrica como GM es correspondiente a la cantidad de vectores característicos independientes. Se puede concebir también como la dimensión del espacio característico asociado.
En el ámbito de la geometría, la multiplicidad también puede referirse a la cantidad de veces que una recta, un plano o una superficie corta o toca a otra figura. Por ejemplo, si una recta toca a una curva en un solo punto, se dice que la multiplicidad de la intersección es 1. Si la recta corta a la curva en dos puntos, la multiplicidad es 2, y así sucesivamente. Este concepto es muy útil en el estudio de las curvas y superficies algebraicas.
