Método de Bairstow

Se trata de un proceso iterativo que combina los métodos de Muller y Newton-Rapshon. Para poder realizarlo, debemos de partir de dos polinomios cuadráticos:

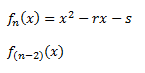
Dados los datos anteriores, debemos seguir estos pasos:

1º) Debemos localizar en el problema fn(x) y r0 y s0 (los valores iniciales)

2º) Ahora, utilizando el método de Newton-Rapshon (explicado en otro artículo) calculamos:

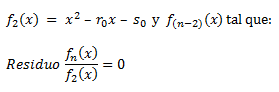
**Nota: Cuando decimos residuo nos referimos al resto de la división, es decir, nos debe de dar un cociente exacto.

3º) Se hallan las raíces f2(x) utilizando la fórmula general

4º) Calculamos:

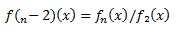
5º) Ahora hacemos:

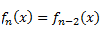
6º) En caso de que el polinomio sea de grado mayor que 3, volvemos al paso 2

7º) En caso contrario, terminamos el ejercicio.

Es importante mencionar que este método es especialmente útil cuando se trata de polinomios de alto grado. En estos casos, los métodos tradicionales pueden ser muy laboriosos o incluso inviables. El método de Bairstow, en cambio, proporciona una forma sistemática y eficiente de abordar estos problemas.

Los pasos anteriormente expuestos sirven para llegar a la solución deseada. El objetivo final es hallar las raíces, tanto las reales como las imaginarias.

Para entender mejor el proceso, es útil considerar un ejemplo. Supongamos que tenemos el siguiente polinomio:

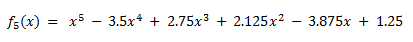
Considérese r0=-1 y s0=-1

1º) Ya sabemos que son r0=-1 y s0=-1, tal como se indica arriba, y anotamos también f5(x).

2º) Aplicamos Ruffini para sacar factor común a ese f5(x):

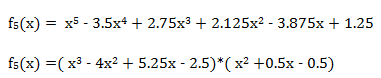
**Nota: Hemos obviado el cálculo por Ruffini, pues ya se ha explicado en otra lección, pero bueno, que sepáis que sale de ahí.

Por tanto, las raíces de x² +0.5x – 0.5=0 son:

x1=0.5

x2=-1

3º) Se hallan ahora las raíces de f2(x), que es la función que nos ha quedado después de hallar las primeras raíces exactas:

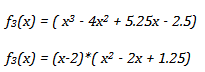
Por tanto, igualando a cero:

x² – 2x +1.25=0

x₃ = 1 + 0.5i

x₄ = -1- 0.5i

** Las «ies» expresan la parte de la solución que es número imaginario, ya que la solución queda con una raíz cuadrada negativa:

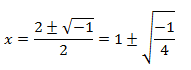
4º) f₁(x) =(x – 2)

Por tanto, la raíz de ese polinomio, igualando a cero: x5=2

Para finalizar, planteamos todas las raíces que hemos ido encontrando:

x = [0.5, 1, (1 + 0.5i), (1 – 0.5i), 2]

Y esta será la solución al ejercicio.

Esperamos que este ejemplo ilustre claramente cómo se aplica el método de Bairstow. Como se puede ver, el proceso es bastante directo una vez que se entienden los pasos. Sin embargo, es importante recordar que la precisión de los resultados depende en gran medida de la elección de los valores iniciales r0 y s0. Por lo tanto, es posible que sea necesario ajustar estos valores y repetir el proceso varias veces para obtener los resultados más precisos.