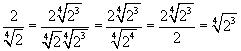Racionalización de radicales
Cuando no es posible simplificar un número para quitar una raíz cuadrada o una raíz cúbica, etc., estamos hablando de un radical. Por ejemplo: √2 (la raíz de 2) no puede simplificarse más, por lo cual es un radical. Pero √4 (la raíz cuadrada de 4) sí es posible simplificarla, así que en este caso no estamos hablando de un radical.
Los radicales tienen infinitas cifras decimales que no se repiten jamás, y por eso son considerados números irracionales. Cuando hablamos de un radical, hacemos referencia a una raíz irracional. Es muy importante tener en claro que no todas las raíces son radicales.
Un radical se expresa de la siguiente forma,
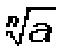
En dicha forma n ∈ N y a ∈ R ; con tal que cuando a sea negativo, n ha de ser impar.
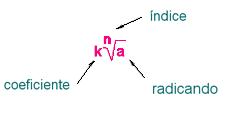
También se puede expresar un radical en forma de potencia:
![]()
En caso de tener fracciones (expresión de una cantidad dividida entre otra) con radicales en el lugar del denominador es conveniente tomar fracciones equivalentes y además que estas no posean radicales en el denominador. En otras palabras la racionalización de radicales es un proceso donde se tiene que eliminar el radical o los radicales, que están en el denominador de la fracción. Este procedimiento es lo que se denomina racionalización de radicales de los denominadores. Dependiendo la clase de radical o la forma en la cual es expresado y que se muestra en el denominador, el procedimiento cambia.
• Cuando el denominador tan solo admite un término, el cual a la vez se forma por tan solo una raíz, bastará con multiplicar el numerador y el denominador por la dicha raíz.
Veamos ahora un ejemplo, si lo que se quiere es proceder a racionalizar la parte del denominador del siguiente quebrado o fracción,
![]()
multiplicamos entonces numerador y el denominador por,
![]()
Entonces,
![]()
Otro ejemplo, al racionalizar la siguiente función,
![]()
Si se extraen los factores posibles en el radical del denominador previo a la racionalización, tedremos que:
![]()
Bastará entonces con la multiplicación del numerador y el denominador por la raíz cuadrada de 2, para descartar y de esta forma Prescindir de la raíz cuadrada del denominador:
![]()
También se puede simplemente proceder a la multiplicación del numerador y del denominador por la raíz cuadrada de 18.
![]()
Entonces se extraen factores de la raíz correspondiente al numerador y se simplifica.
![]()
Como podemos observar, obtuvimos un igual resultante.
• El denominador de la fracción posee dos términos. En uno de esos términos o también en ambos se encuentra claramente una raíz , se procede a multiplicar el numerador y el denominador por la parte conjugada del denominador. Es decir que si se trata de una adición se multiplicará por la sustracción, y viceversa.
Por ejemplo,
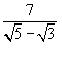
Si se multiplica el numerador y el denominador por,
![]()
Entonces,
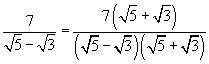
En la parte del denominador siempre estrá presente el resultado de la multiplicación de una adición por una diferencia, lo cual puede expresarse de la siguiente forma,
![]()
Por lo cual tenemos,
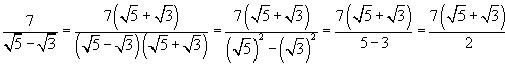
• Si el denominador únicamente posee un término con una raíz de cualquier índice “n” se puede multiplicar numerador y también denominador por una raíz también de índice n que complete una potencia que nuevamente tenga como exponente a “n”.
Por ejemplo,
![]()
Procedemos a Factorizar el radicando perteneciente a la parte del denominador:

multiplicamos numerador y denominador por,
![]()
lo cual completa la potencia del número natural 5,
![]()
Veamos un nuevo ejemplo:
![]()
Si lo que se busca es que la cuarta raíz se elimine, la potencia debe elevarse a 4. Luego será suficiente con realizar una multiplicación,
![]()
Entonces,