Función radical

Vamos a continuar estudiando otro tipo de funciones: las funciones radicales, también conocidas como funciones irracionales; que como su nombre indica son aquella funciones en las que su definición aparece un radical, o lo que es lo mismo una raíz.

En esta ocasión nos vamos a centrar en las raíces cuadradas del tipo: con a y b cualquier número real siempre y cuando a sea distinto de cero.

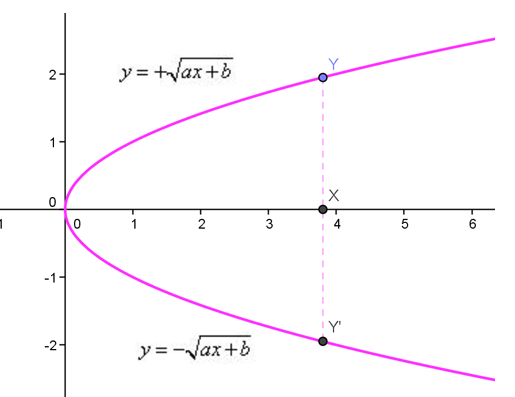
Como ya todos sabemos el resultado de una raíz cuadrada son dos, uno positivo y otro negativo, por tanto, su representación sería de esta forma:

Pero, evidentemente, esta representación no puede ser una función, ya que para una misma absccisa tenemos de valores de y. Por tanto, para llevar a cabo la representación de una función radical de índice dos (o par) tendremos que especificar el signo que vamos a utilizar.

PASOS PARA REPRESENTAR UNA FUNCIÓN RADICAL

1º. En primer lugar, tenemos que determinar el dominio de definición de la función, que como ya sabemos, por tratarse de una raíz cuadrada serán todos los valores de x que hagan que el radicando sea mayor o igual que cero: ax+b≥0, luego serán todos los valores de x tales que: x≥-b/a, (recordad llevad cuidado a la hora de despejar la x, porque como ya sabemos en las inecuaciones si a es negativa cambia el signo de la desigualdad).

2º. Una vez conocido los valores de x para los cuales existe función, tendremos que mirar si nuestra función es positiva o negativa, lo cual dependerá del signo de la raíz que hayamos elegido.

3º. Por último, comenzando en el punto (-b/a, 0), ya sea hacia la derecha o hacia la izquierda, en la parte positiva o negativa, realizaremos un boceto de la función similar al de la imagen anterior. Si es necesario siempre podemos realizar una tabla de valores.

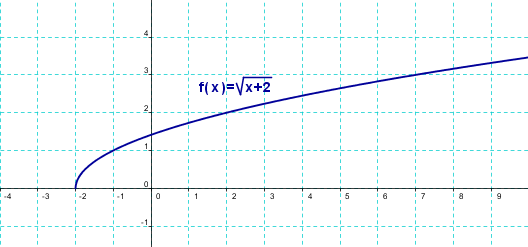
Como podemos ver en la siguiente representación, cuyo dominio es x≥-2, y es una función positiva.

Al igual que ocurría con las funciones racionales, también las funciones radicales sufren traslaciones:

TRASLACIONES

-Transformación vertical: Si sumas o restas un número k a nuestra raíz, la representación se traslada hacia arriba o hacia abajo respectivamente. En este caso el punto de partida de nuestra representación será (-b/a, k).

-Transformación horizontal: Si al valor de x le sumamos o restamos un número k, se traslada hacia la izquierda o derecha respectivamente, como podemos observar en el ejemplo anterior. Supongamos que partimos de la función raíz de x, si queremos representar la raíz de x+2, estamos trasladando la función 2 unidades hacia la izquierda.

-Comprensión o estiramiento: Si multiplicamos la raíz por un valor k, nuestro representación se estira o comprime. Se estirará cuando k>1, y se comprimirá cuando 0<k<1.

Además de estas transformaciones básicas, es importante mencionar que las funciones radicales también pueden experimentar reflexiones. Una reflexión sobre el eje x se produce cuando multiplicamos la función por -1. Por ejemplo, si tenemos la función f(x) = √x, su reflexión sería f(x) = -√x. Esta transformación invierte la función sobre el eje x, cambiando todos los valores positivos de y a negativos.

Otra transformación interesante es la reflexión sobre el eje y, que se obtiene al sustituir x por -x en la función. Por ejemplo, si tenemos la función f(x) = √x, su reflexión sobre el eje y sería f(x) = √(-x). Sin embargo, es crucial tener en cuenta el dominio de la función, ya que la raíz cuadrada de un número negativo no está definida en el conjunto de los números reales.

Por último, es importante mencionar que las funciones radicales también pueden combinarse con otras funciones para formar funciones más complejas. Por ejemplo, podemos tener una función radical dentro de una función polinómica o una función exponencial. Estas combinaciones pueden resultar en gráficos interesantes y complejos que requieren un análisis cuidadoso para determinar su dominio, rango y comportamiento general.

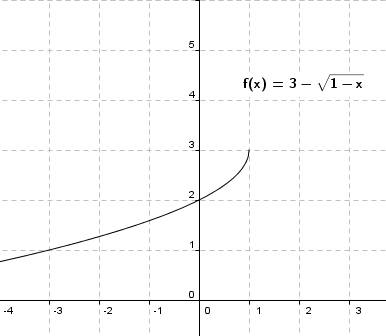
Por último, para vamos a representar la siguiente función: a partir de transformaciones en la función – raíz de x.

1º. Como sabemos, la función negativa de la raíz cuadrada se encuentra en la parte negativa.

2º. El dominio de la función que tenemos que representar es (-∞,1], por tanto,nuestra función viene del menos infinito y terminaría en el punto (1,0).

3º. Como tenemos 3 unidades sumando a la raíz inicial, la función se traslada de forma vertical 3 unidades hacia arriba, y por tanto el punto donde termina es el (1,3)