Norma vectorial

Un espacio vectorial es el objeto básico de estudio en álgebra lineal. A los elementos de los espacios vectoriales se les llama vectores. Sobre los vectores se pueden realizar dos tipos de operaciones:

La multiplicación por escalares y la adición. Es importante conocer la longitud de los vectores. Para esto es necesario definir un operador norma que determine la longitud o magnitud del vector.

El vector está comprendido por los siguientes elementos. La Dirección que determinada por la recta de soporte y puede ser vertical, horizontal e inclinada u oblicua. La orientación o sentido que esta determinada por la flecha y puede ser horizontal hacia la derecha o hacia la izquierda, vertical hacia arriba o hacia abajo e inclinada ascendente o descendente hacia la derecha o hacia la izquierda. El punto de aplicación, que esta determinado por el punto origen del segmento que forma el vector y por último la longitud o módulo, es el número positivo que representa la longitud del vector.

La definición general de norma se basa en generalizar a espacios vectoriales abstractos el concepto de módulo de un vector de un espacio euclídeo. En un espacio no euclídeo la noción de camino más corto entre dos puntos no es mas identificable con el de la línea recta; por lo cual, se recurre a las propiedades operacionales de la norma euclídea. Definamos entonces lo que es una norma euclidea. En un espacio euclídeo los vectores son representados como segmentos orientados entre puntos del espacio (euclideo). Dado un vector de un espacio vectorial euclídeo, la norma de un vector es definida como la distancia (en línea recta) entre dos puntos A y B que delimitan al vector. Coincidiendo en un espacio euclídeo la norma de un vector con el módulo del vector AB.

• En dos dimensiones:

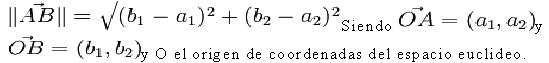
• Ampliando lo anterior al espacio euclídeo de tres dimensiones, es de igual forma elemental que:

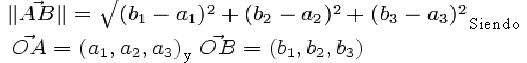
• En el caso general de un espacio euclídeo de n dimensiones se tiene qué :

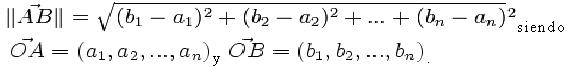
De esto se sigue que, fijada una base ortonormal B en la cual un vector V se da a partir de sus componentes en esta base, VB=(v1,v2…..,vn), la norma de dicho vector vendrá dada por:

De la norma euclidea se extraen entonces las condiciones que debe cumplir la «longitud de un vector», o norma vectorial, en un espacio vectorial. Estas condiciones siempre son positivas e independientes de la orientación de la medición. La longitud es directamente proporcional al tamaño y entre dos puntos será menor o igual que la suma de longitudes desde esos mismos dos puntos a un tercero distinto de ellos. Dichas condiciones generan la siguiente definición matemática:

Decimos que :

es un operador que define la norma del vector x, y lo expresamos como, si cumple lo siguiente:

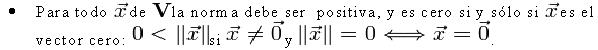
(esto sería una desigualdad triangular, la suma de dos lados de un triángulo nunca es menor que el tercer lado).

Cualquier operador que cumpla con las tres condiciones que hemos visto es un operador norma. A continuación tenemos ejemplos de algunos posibles operadores norma.

Así, para el caso p = 1 obtenemos:

Mientras que para el caso p = 2 obtenemos la norma euclídea explicada más arriba.

• Otro operador norma sería, la norma del supremo:

Para un espacio de dimensión finita numerable se podría escribir:

La elección del subíndice ∞ para esta norma se debe al hecho de que:

El estudio de los vectores lleva consigo un extenso lugar de trabajo ya que tiene influencia en áreas de trabajo que antes eran desconocidas por nosotros.